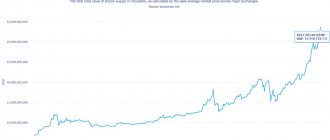
Со времен возникновения письменности и до середины XX века криптография была искусством. Сейчас это не только проработанная область науки на стыке математики и информатики, но и то, чем мы пользуемся ежедневно. К чему может привести незнание криптографии и любовь к халяве, как прочитать вашу переписку, почему шифрование на открытых ключах безопаснее и что значит cLhmGccA4aSaRslIsnA, рассказывает кандидат физико-математических наук, лектор по защите информации в МФТИ Сергей Владимиров.
Классическая криптография, или Искусство сохранять голову
Сергей Владимиров
Один из самых простых способов скрыть информацию — заменить каждую букву алфавита на другие буквы того же алфавита. Понятно, что так называемый шифр Цезаря, где каждая буква письма заменялась на букву, отстоящую по алфавиту на три позиции дальше, был не очень надежной криптосистемой. Так что чтобы расшифровать такой текст, достаточно знать алгоритм замены.
Существует и другой способ получить зашифрованный текст, или шифротекст, — заменить буквы одного алфавита на буквы другого алфавита или на картинки, как в «Пляшущих человечках» Конан Дойля. Чтобы прочитать такой текст, требуется ключ, соотносящий два алфавита между собой (или криптоаналитические способности Шерлока Холмса). Прием, который помог вымышленному гению взломать шифр, был описан еще в VIII веке арабским филологом аль-Фарахиди в «Книге тайного языка». Он верно предположил, что зашифрованное письмо начинается со стандартной фразы «Во имя Аллаха», и это помогло ему разгадать все остальное. В более поздних арабских трактатах впервые упоминается частотный криптоанализ — сопоставление самых часто употребляемых букв алфавита с самыми часто встречающимися в шифротексте символами. Над созданием устойчивого к частотному криптоанализу шифра бились многие европейские криптографы эпохи Возрождения. Например, заменяли не на одну букву, а на две или больше. Техники шифрования тех времен дали основу для более современных криптосистем.
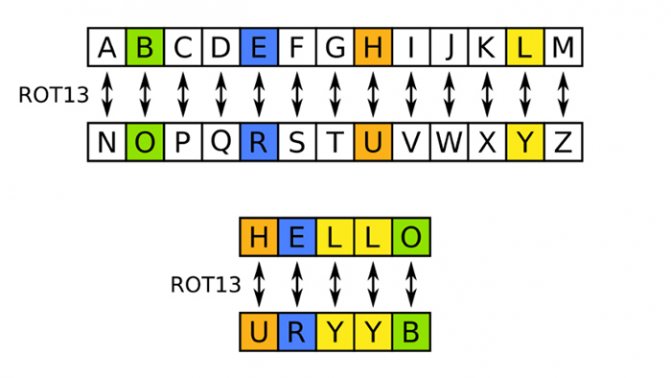
Шифром Цезаря со сдвигом 13 скрывают спойлеры и ругательства на интернет-форумах
Средние века
В средневековье люди продолжили использовать моноалфавитные шифры, хотя в некоторых странах изобретали и другие способы криптографии. Но если раньше шифровали в основном военные послания, то теперь засекречивать сообщения стали дипломаты, купцы и простые граждане.
«Шифры усложнялись по мере распространения техники частотного криптоанализа — когда шифр смогли разгадать без ключа, анализируя, как часто в засекреченном тексте встречаются разные буквы. Впервые эта технология появилась в арабских странах. Ее развитие привело к появлению полиалфавитных шифров – это тот же самый шифр простой замены, но на основе нескольких алфавитов, и шифров – замены букв по определенным правилам», – отмечает Евгений Жданов.
Манускрипт аль-Кинди, IX век. С VIII столетия нашей эры криптография быстрее развивается в арабских странах. Одни из первых трудов, в которых говорится о дешифровке моноалфавитных и полиалфавитных шифров написаны арабскими учеными. Важный труд того времени — «Манускрипт о дешифровке криптографических сообщений» ученого аль-Кинди. Именно он первым упомянул о частотном анализе шифров.
Первая страница манускрипта аль-Кинди / ©Википедия
Литорея, 1300 год. «Удивительно, но криптография существовала и в Древней Руси – факт малоизвестный, но крайне интересный. В древнерусской литературе использовалось тайнописание, называемое Литорея. Она могла быть простой и мудрой. Простая напоминала тарабарскую грамоту, мудрая — шифр простой замены некоторых букв точками, палками, кругами, которые означали разряд числа», – говорит эксперт.
Пример использования простой литореи с алфавитом русского языка. Согласные буквы располагали в два ряда, гласные оставались на своих местах / ©Пресс-служба Ростеха Чтобы зашифровать послание, в исходном слове нужно заменить только согласные по двурядной таблице выше: букве «Б» соответствует «Щ», «Ш» — «В» и так далее / ©Пресс-служба Ростеха
Криптография Византии. Историкам известно о нескольких способах засекретить послания, которые использовали в Византии. В основном, это были простые приемы: скоропись, замена алфавита, неправильное написание букв, лигатурное письмо. Встречались и усложненные, которые назвали цифровой тайнописью: когда буквам присваивали числовое значение и шифровали текст с помощью арифметических действий: числа раскладывали на слагаемые, прибавляли и вычитали.
«В Средние века прорыва в шифровании не произошло. Новые и более сложные методы шифрования появлялись редко – старых было вполне достаточно. Тем не менее, Средневековье внесло свой вклад в науку о криптографии», – резюмирует Евгений Жданов.
Современная криптография, или Наука защищенного общения
Криптография сильно повлияла на ход Второй мировой войны. В начале XX века появились электромеханические шифровальные машины, в том числе знаменитая немецкая «Энигма», однако криптография все еще оставалась искусством, а не наукой. Одна из первых шифровальных школ для математиков появилась в Польше: первые успехи по взлому «Энигмы» принадлежат ее ученикам. Мариан Реевский, применив математические методы, сумел разгадать логическую структуру «Энигмы», однако немцы совершенствовали машину, и задача расшифровки все время усложнялась. После захвата Польши криптографические наработки передали в британский Блетчли-парк, где работала команда британских математиков, в том числе Алан Тьюринг. С помощью Turing Bombe, разведки, стандартных фраз и ошибок противника «Энигму» удалось взломать, тем самым приблизив окончание войны где-то на два года. С современной точки зрения шифровальный механизм был не очень надежен, хотя немцы считали иначе. Для взлома следующей криптомашины уже пришлось разработать первый электронный компьютер.


Ротор «Энигмы»
Англия не повторяла ошибки поляков и тщательно скрывала, что немецкие сообщения расшифровываются, иначе шифр снова мог бы поменяться и преимущество перешло бы на сторону фашистов. Когда из тайной переписки немцев стало известно, что планируется бомбардировка английского города Ковентри, Уинстону Черчиллю пришлось сделать тяжелый выбор и пожертвовать жилым городом ради сохранения тайны.
После войны математик Клод Шеннон опубликовал научные труды, которые положили начало развития криптографии как точной математической науки. В частности, принцип Керкгоффса, французского офицера XIX века, гласит: «Стойкость криптосистемы не должна зависеть от секретности алгоритма». То есть предполагается, что взломщик знает, каким образом открытый текст (текст до шифрования) преобразуется в закрытый (шифротекст). Но ключ, с помощью которого это делается, должен оставаться тайной. Взломать такую систему можно простым перебором ключа, именно поэтому важно, чтобы ключ был не слишком коротким и чтобы был один-единственный способ понять, что он правильный.
В то же время слишком большой ключ отнимает непозволительно много вычислительных ресурсов, даже для современных машин. В 70-х годах прошлого века компьютеры и обмен информацией только начали входить в жизнь обычных американцев. Тогда существовало много разных способов шифрования, но не было единого стандарта, как когда-то не было стандарта 220В для розеток. Разработать стандарт шифрования поручили фирме IBM, которая с приходом Хорста Фейстеля представила общественности первый стандарт государственного уровня — DES (Data Encryption Standard) на блочных шифрах. Принятый как временная мера DES продержался до 2002 года, после чего его заменили более надежным AES (Advanced Encryption Standard). В России первый стандарт ввели в 1990 году, он тоже работал на блочных шифрах, сейчас же действует ГОСТ Р 34.10-2012, основанный на эллиптических кривых.
Эпоха шифровальных машин
Промышленная революция не обошла вниманием и криптографию. Около 1790 года один из отцов – основателей США Томас Джефферсон создал дисковый шифр, прозванный позже цилиндром Джефферсона. Этот прибор, основанный на роторной системе, позволил автоматизировать процесс шифрования и стал первым криптоустройством Нового времени.


Шифровальный цилиндр Томаса Джефферсона
Большое влияние на шифровальное дело оказало изобретение телеграфа. Прежние шифры вмиг перестали работать, при этом потребность в качественном шифровании только возрастала в связи с чередой крупных военных конфликтов. В XIX-XX веках основные импульсы для развития криптографии давала именно военная сфера. С 1854 года британские военные применяют шифр Плейфера, в основе которого – шифрование биграмм, или пар символов. Этот шифр использовался до начала Второй мировой войны.
Во Второй мировой войне противники уже использовали мобильные электромеханические шифраторы, шифры которых считались нераскрываемыми. Устройства были роторными или на цевочных дисках. К первым относилась знаменитая машина «Энигма», которой пользовались нацисты, ко вторым – американская машина M-209.
Принцип работы «Энигмы» заключался в следующем: при каждом нажатии на клавишу с буквой алфавита в движение приходили один или несколько роторов. Буква изменялась несколько раз по принципу шифра Цезаря, и в окошке выдавался результат. Шифры «Энигмы» считались самыми стойкими для взлома, так как количество ее комбинаций достигало 15 квадриллионов. Однако код «Энигмы» все же был расшифрован, сперва польскими криптографами в 1932 году, а затем английским ученым Аланом Тьюрингом, создавшим машину для расшифровки сообщений «Энигмы» под названием «Бомба». Комплекс из 210 таких машин позволял англичанам расшифровывать до 3 тыс. военных сообщений нацистов в сутки и внес большой вклад в победу союзников.


Роторы «Энигмы» в собранном состоянии. Фото: wikimedia.org
О советских шифровальных машинах известно мало, так как до последнего времени информация о них была засекречена. Например, до 1990-х годов в СССР и союзных странах использовалась роторная шифровальная машина «Фиалка». В отличие от «Энигмы» и других устройств, в ней использовались 10 роторов, а информация выводилась на бумажную ленту.
Два ключа лучше, чем один
В конце 1970-х — начале 1980-х годов интерес общественности к криптографии вырос настолько, что государственные службы обеспокоились, как бы надежные способы шифрования не попали в руки террористов и преступников, и попытались подавить гражданскую (или открытую) криптографию. Однако череда принятых мер и законов не была успешной. Так, криптосистема RSA, разработанная Ривестом ®, Шамиром (S) и Адлеманом (A) в 1977 году, несмотря на первоначальные препятствия АНБ, сейчас используется практически везде. Она обладает интересным криптографическим свойством, которое можно понять, для начала познакомившись с так называемыми симметричными системами шифрования. В симметричной криптографии для шифрования и дешифрования используется один и тот же ключ. Эти простые алгоритмы идеологически описаны еще в 50-х, но всем им свойственен один большой недостаток. Представим, что Боб и Алиса общаются в школе с помощью шифра. Тогда, чтобы создать секретный канал связи, им сначала нужно найти безопасный канал для передачи ключа, например дупло дерева в парке. Возникает вопрос, почему бы им тогда просто не класть туда записки? Эту проблему симметричного шифрования называют проблемой распространения ключей.
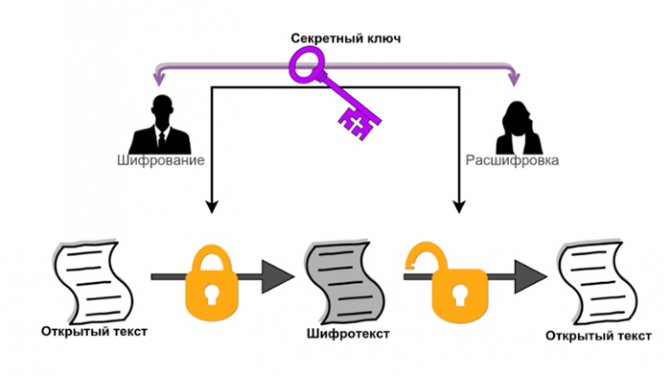

RSA считается первой реальной системой, которая использует шифрование на открытых ключах, или асимметричное шифрование. В этом случае у Боба есть два ключа, один закрытый (private key), а другой распространяется по открытому каналу и даже написан на визитке Боба (public key). Тогда зашифровать сообщение для Боба с помощью открытого ключа может любой, но расшифровать может только Боб, потому что закрытый ключ он никому не показывает. Для наглядности рассмотрим такой пример: пусть в телефонной книге 264 фамилии. Чтобы зашифровать текст, поочередно берем каждую букву текста, выбираем любую фамилию на эту букву и записываем номер. Теоретически, расшифровать такое послание может каждый, у кого есть такая книга, но для этого ему придется пролистать ее всю, с 20-значным числом фамилий. У легального же пользователя, которому посылается это сообщение, есть закрытый ключ — такая же книга, но отсортированная не в алфавитном порядке, а по номерам.
Этот пример показывает, что ни одна криптографическая система не является идеально надежной — всегда можно взять и отсортировать телефонную книгу по номерам. Только это займет очень-очень много времени. При современных алгоритмах криптосистемы на открытых ключах взламываются за время большее, чем время существования Вселенной, но теоретически это возможно.
Криптография для всех
В 1949 году Клод Шеннон пишет работу «Теория связи в секретных системах», и криптография окончательно переходит в сферу математики. К концу 1960-х роторные шифровальные системы заменяются более совершенными блочными, которые предполагали обязательное применение цифровых электронных устройств. В 1967 году ученый Дэвид Кан издал популярную книгу «Взломщики кодов», которая вызвала большой интерес к криптографии.
С распространением компьютеров криптография выходит на новый уровень. Мощности новых устройств позволяют создавать на порядки более сложные шифры. Шифр или код становится языком общения между компьютерами, а криптография становится полноценной гражданской отраслью. В 1978 году разрабатывается стандарт шифрования DES, который стал основой для многих современных криптографических алгоритмов.
Сфера использования криптографии расширяется, при этом власти различных стран пытаются удержать контроль над использованием шифров. Разработки криптографов засекречиваются, от производителей шифровальных машин требуют оставлять в продуктах «черные ходы» для доступа спецслужб.


Параллельно независимые криптоаналитики разрабатывают способы шифрования, которыми могли бы пользоваться все желающие – так называемую открытую криптографию. Особенно актуально это стало с развитием интернета, где вопрос конфиденциальности информации встал очень остро. Первой криптосистемой с открытым ключом считается созданный в 1977 году алгоритм RSA, название которого является акронимом имен создателей – Риверста, Шамира и Адельмана. А в 1991 году американский программист Филипп Циммерман разрабатывает популярнейший пакет PGP с открытым исходным кодом для шифрования электронной почты.
Распространение доступного интернета по всему миру невозможно представить без криптографии. С появлением мессенджеров, социальных сетей, онлайн-магазинов и сайтов государственных услуг передача персональной информации в сети происходит без остановки и в огромных количествах. Сегодня мы сталкиваемся с криптографией ежедневно, когда вводим пароль от почтового сервиса, узнаем статус покупки онлайн или делаем денежный перевод через приложение банка. Криптография прошла гигантский путь от простых шифров древности к сложнейшим криптосистемам. Будущее этой науки творится на наших глазах – очередная революция в шифровании произойдет с появлением квантовых суперкомпьютеров, разработка которых уже ведется.
Мультипаспорт
Криптографически стойкая хэш-функция преобразует исходный текст в одну строчку так, что из этой строчки невозможно (или очень сложно) получить исходный текст. Хэш-функцию используют, например, там, где нужно вводить пароль: фразу в строке ввода сравнивают не с самим паролем, а с его хэш-функцией.
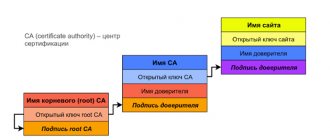
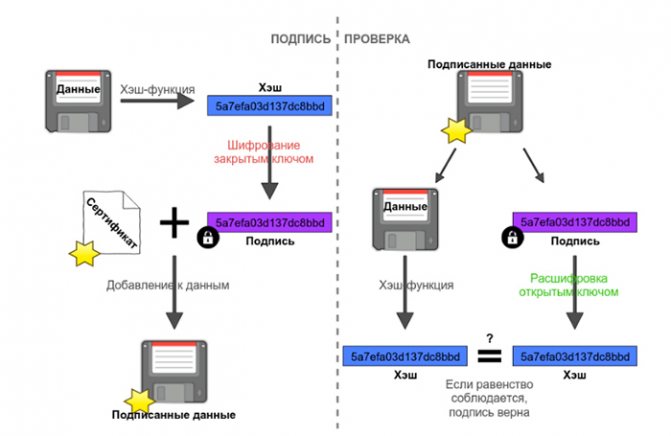
Проверить, не исказилась ли информация во время передачи по зашифрованному каналу можно с помощью электронной цифровой подписи (digital signature). В этом случае Алиса зашифровывает текст своим закрытым ключом и вместе с открытым текстом отправляет Бобу. Если Боб расшифрует шифротекст открытым ключом Алисы и он совпадет с не зашифрованным текстом, то все хорошо. На практике закрытым ключом обычно зашифровывается хэш-функция документа. Но что если злоумышленник выдает свой открытый ключ за открытый ключ Алисы? Чтобы ему помешать, электронная подпись помимо прочего содержит так называемый сертификат открытого ключа, выданный доверенным центром сертификации (CA, сertification authority), который имеет данные по всем открытым ключам и их пользователям. Сертификат, в свою очередь, тоже должен быть подписан. Важно, что открытый ключ доверенного центра должен быть известен заранее, иначе его тоже можно подделать.

Идеальный шифр
Но один шифр оказался особенным. One-time pad (OTP, «одноразовый блокнот»), или шифр Вернама, предложенный для телеграфных сообщений сотрудником AT&T, оказался абсолютно стойким к любому криптоанализу. Это было доказано в 1940-х годах великим математиком и инженером Шенноном. В чем подвох? Рассмотрим, как такой шифр устроен.
В отличие от выше описанных алгоритмов, описанных для текстов на естественном языке, OTP можно описать только для двоичного (бинарного) кода. В современных компьютерах и прочих электронных устройствах для представления текста чаще всего используется кодировка ASCII и совместимая с ней UTF-8. Но двоичные кодировки появились задолго до двоичных компьютеров — они использовались в телеграфах. Стандартом в США в то время был код Бодо.
Итак, у нас есть исходный текст — строка (последовательность) битов (цифр 0 и 1 — «bit» значит «binary digit», двоичная цифра). Все, что делает шифр Вернама — объединяет эту строку с секретным ключом. Побитово. Операцией «исключающее ИЛИ», XOR, она же «сложение по модулю 2». 0 ⊕ 0 = 0. 0 ⊕ 1 = 1. 1 ⊕ 0 = 1. 1 ⊕ 1 = 0. (Благодаря симметричности такой операции, расшифровка происходит точно так же, как и шифрование.)
Из этого следует то, что ключ должен быть битовой строкой такой же длины, как исходное сообщение. А еще он должен быть случайным и использоваться только один раз (и, конечно, оставаться тайным). Вся безопасность шифра полагается на эти требования.
Собственно необходимость иметь достаточно длинный ключ — главная причина того, что OTP не используется в современных компьютерных системах. Ну разве кто-то захочет хранить ключ объемом 1 Гигабайт, чтобы защитить данные такого же объема? Да и где взять длинные случайные числа?
Впрочем, принцип одноразового блокнота лежит в основе одного из двух видов современных шифров — поточных шифров (stream ciphers). Вместо длинного ключа используется последовательность, созданная криптографически стойким генератором псевдослучайных чисел — маленький ключ (обычно — случайная последовательность из 128 или 256 бит) «растягивается» с помощью алгоритма до огромной длины. А идея применения сложения по модулю 2 все та же.
Зеленый замочек
Когда вы запрашиваете страницы таких сервисов, как «ВКонтакте», Google, «Одноклассники», Facebook и многих других, адрес в браузерной строке начинается с https://, а рядом с ним стоит зеленый замочек. Что это значит? HTTPS отличается от HTTP тем, что данные передаются с помощью криптографических протоколов SSL и TLS. Это означает, что когда вы заходите на тот же «ВКонтакте», вся информация, которой вы обмениваетесь с собеседником, шифруется. Вторая важная особенность протокола состоит в том, что он пытается гарантировать, что это действительно тот сайт, на который вы хотели зайти. Если вы послали запрос и установили соединение с легальным «ВКонтакте», то вам придет сертификат открытого ключа, который содержит все параметры шифрования между вами и сервером. Сертификат открытого ключа должен быть подписан доверенным центром (CA), а сертификат доверенного центра, в свою очередь, должен быть подписан корневым доверенным центром (root CA). Так получается цепочка сертификатов, или цепочка доверия. Честными должны быть все члены цепочки, а корневой центр должен иметь широко известный открытый ключ. Таких корневых центров немного, и все их открытые ключи зашиты в браузер. Чтобы браузер показал зеленый замочек, в конце цепочки сертификатов должен находиться сертификат корневого центра, известного браузеру. Чтобы подделаться под «ВКонтакте» или «Одноклассники», злоумышленнику придется подделать цифровую подпись корневого доверенного центра. Подделать цифровую подпись почти нереально, ведь для этого нужно знать закрытый ключ корневого доверенного центра. Поэтому соединение HTTPS защищает от компьютерных атак. Но это в теории, а как на практике?
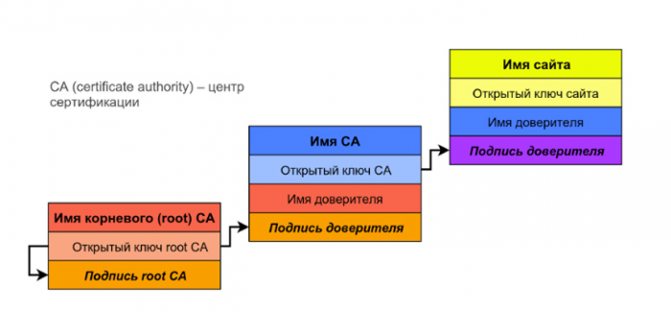

Цепочка доверия на примере сертификатов SSL
Исторические шифры и первые шифраторы
Согласно источникам, первые способы шифрования текста появились вместе с зарождением письменности. Способы тайного письма применялись древними цивилизациями Индии, Месопотамии и Египта. В письменах Древней Индии упоминаются способы изменения текста, которые использовали не только правители, но и ремесленники, желающие скрыть секрет мастерства. Истоком криптографии считается использование специальных иероглифов в древнеегипетской письменности около четырех тысячелетий назад.
Первым шифром, зародившимся в древних цивилизациях и актуальным, в некотором роде, и по сей день, можно считать шифр замены. Чуть позже был придуман шифр сдвига, который применялся Юлием Цезарем, почему и был назван в его честь.
Помимо шифров, нельзя не упомянуть о приборах для шифрования, которые разрабатывали древние математики. Например, скитала — первый шифратор, разработанный в Спарте. Представлял собой палку, на которую по всей длине наматывалась лента пергамента. Текст наносился вдоль оси палки, после чего пергамент снимался, и получалось шифрованное сообщение. Ключом служил диаметр палки. Однако такой способ шифрования был абсолютно нестойким — автором взлома стал Аристотель. Он наматывал ленту пергамента на конусообразную палку до тех пор, пока не появлялись отрывки читаемого текста.
Также ярким примером из мира древних шифраторов может стать диск Энея — диск с отверстиями по количеству букв в алфавите. Нитка протягивалась последовательно в те отверстия, которые соответствовали буквам сообщения. Получатель вытаскивал нитку, записывал последовательность букв и читал секретное послание. Однако этот шифратор обладал существенным недостатком — достать нитку и разгадать послание мог кто угодно.
Шифр сдвига
Это один из самых первых типов шифра. Процесс шифрования очень прост. Он заключается в замене каждой буквы исходного сообщения на другую, отстоящую от исходной на заданное количество позиций в алфавите. Это количество позиций называется ключом. При ключе, равном трем, этот метод называется шифром Цезаря. Император использовал его для секретной переписки. Для того чтобы зашифровать сообщение, нужно построить таблицу подстановок:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c |
Как видишь, во втором ряду символы алфавита сдвинуты на три позиции «назад». Чтобы зашифровать сообщение, для каждого символа исходного текста нужно взять соответствующий ему символ из таблицы подстановки.
Пример шифра
Исходный текст: Hi, Brut! How are you? Шифрованный текст: Kl, Euxw! Krz duh brx?
Расшифрование
На этапе расшифрования мы имеем шифрованный текст и ключ, равный трем. Чтобы получить исходный текст, ищем для каждого символа сдвиг на три позиции к началу алфавита. Так, для первого символа K сдвиг три будет означать символ H. Далее посимвольно расшифровываем текст, пока не получаем исходную фразу Hi, Brut! How are you?.
Криптоанализ
Легче всего такой шифр взломать простым перебором всех возможных значений ключа — их всего 25. Здесь все просто, и останавливаться смысла нет.
Другой вариант — использовать частотный анализ текста. Для каждого языка есть статистическая информация о частоте употребления каждой буквы алфавита и наиболее часто встречающихся сочетаний букв. Для английского, например, среднестатистические частоты употребления букв таковы:
| e 0,12702 | s 0,06327 | u 0,02758 | p 0,01929 | q 0,00095 |
| t 0,09056 | h 0,06094 | m 0,02406 | b 0,01492 | z 0,00074 |
| a 0,08167 | r 0,05987 | w 0,02360 | v 0,00978 | |
| o 0,07507 | d 0,04253 | f 0,02228 | k 0,00772 | |
| i 0,06966 | l 0,04025 | g 0,02015 | j 0,00153 | |
| n 0,06749 | c 0,02782 | y 0,01974 | x 0,00150 |
Что касается двухбуквенных сочетаний (биграмм), то можно заметить следующую тенденцию:
| Биграмма | Процентное содержание | Биграмма | Процентное содержание |
| th | 3,15 | he | 2,51 |
| an | 1,72 | in | 1,69 |
| er | 1,54 | re | 1,48 |
| es | 1,45 | on | 1,45 |
| ea | 1,31 | ti | 1,28 |
| at | 1,24 | st | 1,21 |
| en | 1,20 | nd | 1,18 |
Идея в том, что в зашифрованном тексте самой часто встречаемой буквой будет не эталонная e, а что-то другое. Соответственно, нам нужно найти самую часто встречаемую букву в нашем шифре. Это и будет зашифрованная е. А дальше нужно подсчитать ее сдвиг от е в таблице подстановок. Полученное значение и есть наш ключ!
Шифр замены
Основной недостаток шифра сдвига заключается в том, что есть всего 25 возможных значений ключа. Даже Цезарь начал подозревать, что его шифр не самая лучшая идея. Поэтому на смену ему пришел шифр замены. Для того чтобы воспользоваться этим алгоритмом, создается таблица с исходным алфавитом и, непосредственно под ним, тот же алфавит, но с переставленными буквами (или любой другой набор знаков):
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| b | e | x | g | w | i | q | v | l | o | u | m | p | j | r | s | t | n | k | h | f | y | z | a | d | c |
Пример шифра
Действуем аналогично предыдущему шифру. Для каждого символа исходного текста берем соответствующий ему из таблицы подстановки:
Исходный текст: Hi, Brut! How are you? Шифрованный текст: Vl, Enfh!Vrz bnw drf?
Расшифрование
При расшифровании заменяем каждый символ шифротекста соответствующим символом из известной нам таблицы подстановки: v => h, l => i и так далее. После чего получаем исходную строку Hi, Brut! How are you?.
Криптоанализ
Криптоанализ этого шифра также выполняется методом частотного анализа текста. Рассмотрим пример:
MRJGRJ LK HVW XBSLHBM RI QNWBH ENLHBLJ, LHK SRMLHLXBM, WXRJRPLX, BJG XRPPWNXLBM XWJHNW. LH LK RJW RI HVW MBNQWKH XLHLWK LJ HVW ZRNMG BJG HVW MBNQWKH XLHD LJ WFNRSW. LHK SRSFMBHLRJ LK BERFH 8 PLMMLRJ. MRJGRJ LK GLYLGWG LJHR KWYWNBM SBNHK: HVW XLHD, ZWKHPLJKHWN, HVW ZWKH WJG, BJG HVW WBKH WJG. HVW VWBNH RI MRJGRJ LK HVW XLHD, LHK ILJBJXLBM BJG EFKLJWKK XWJHNW. JFPWNRFK EBJUK, RIILXWK, BJG ILNPK BNW KLHFBHWG HVWNW, LJXMFGLJQ HVW EBJU RI WJQMBJG, HVW KHRXU WAXVBJQW, BJG HVW RMG EBLMWD. IWZ SWRSMW MLYW VWNW, EFH RYWN B PLMMLRJ SWRSMW XRPW HR HVW XLHD HR ZRNU. HVWNW BNW KRPW IBPRFK BJXLWJH EFLMGLJQK ZLHVLJ HVW XLHD. SWNVBSK HVW PRKH KHNLULJQ RI HVWP LK HVW KH. SBFM\’K XBHVWGNBM, HVW QNWBHWKH RI WJQMLKV XVFNXVWK. LH ZBK EFLMH LJ HVW 17HV XWJHFND ED KLN XVNLKHRSVWN ZNWJ. HVW HRZWN RI MRJGRJ ZBK IRFJGWG ED OFMLFK XBWKBN BJG LJ 1066 NWEFLMH ED ZLMMLBP HVW XRJTFWNRN. LH ZBK FKWG BK B IRNHNWKK, B NRDBM SBMBXW, BJG B SNLKRJ. JRZ LH LK B PFKWFP.
Частотный анализ букв этого шифра показывает следующее (читай построчно, буквы сортированы по частоте использования):
W — 88, H — 74, L — 67, J — 55, B — 54, K — 52, R — 51, N — 41, M — 36, V — 35, X — 29, G — 27, F — 23, P — 16, S — 16, I — 15, Z — 13, E — 13, D — 11, Q — 10, U — 5, Y — 4, T — 1, O — 1, A — 1
Вероятно, что W => e, так как это самая часто встречающаяся буква в шифре (смотри таблицу среднестатистических частот использования букв для английского языка в предыдущем шифре).
Дальше пробуем найти наиболее короткое слово, куда входит уже известная нам буква W => e. Видим, что сочетание HVW чаще всего встречается в шифре. Нетрудно догадаться, что, скорее всего, это триграмма the, то есть в тексте мы уже определили три символа. Если посмотреть на промежуточный результат, сомнений не остается:
MRJGRJ LK the XBSLtBM RI QNeBt ENLtBLJ, LtK SRMLtLXBM, eXRJRPLX, BJG XRPPeNXLBM XeJtNe. Lt LK RJe RI the MBNQeKt XLtLeK LJ the ZRNMG BJG the MBNQeKt XLtD LJ eFNRSe. LtK SRSFMBtLRJ LK BERFt 8 PLMMLRJ. MRJGRJ LK GLYLGeG LJtR KeYeNBM SBNtK: the XLtD, ZeKtPLJKteN, the ZeKt eJG, BJG the eBKt eJG. the heBNt RI MRJGRJ LK the XLtD, LtK ILJBJXLBM BJG EFKLJeKK XeJtNe. JFPeNRFK EBJUK, RIILXeK, BJG ILNPK BNe KLtFBteG theNe, LJXMFGLJQ the EBJU RI eJQMBJG, the KtRXU eAXhBJQe, BJG the RMG EBLMeD. IeZ SeRSMe MLYe heNe, EFt RYeN B PLMMLRJ SeRSMe XRPe tR the XLtD tR ZRNU. theNe BNe KRPe IBPRFK BJXLeJt EFLMGLJQK ZLthLJ the XLtD. SeNhBSK the PRKt KtNLULJQ RI theP LK the Kt. SBFM\’K XBtheGNBM, the QNeBteKt RI eJQMLKh XhFNXheK. Lt ZBK EFLMt LJ the 17th XeJtFND ED KLN XhNLKtRSheN ZNeJ. the tRZeN RI MRJGRJ ZBK IRFJGeG ED OFMLFK XBeKBN BJG LJ 1066 NeEFLMt ED ZLMMLBP the XRJTFeNRN. Lt ZBK FKeG BK B IRNtNeKK, B NRDBM SBMBXe, BJG B SNLKRJ. JRZ Lt LK B PFKeFP.
Отлично, уже известны три буквы. Снова ищем наиболее короткие слова с новыми известными нам подстановками. Сочетание it является частоупотребляемым, и, поскольку буква t уже дешифрована (HVW => the), очевидно, что в нашем тексте L => i (LH => it). После этого обращаемся к поиску биграмм is и to, устанавливаем, что K => s, R => o. Затем обращаем внимание на триграммы ~ing и and. Анализ текста показывает, что BJG, скорее всего, шифротекст от and. После замены всех наиболее часто встречающихся символов получаем текст:
Mondon is the XaSitaM oI QNeat ENitain, its SoMitiXaM, eXonoPiX, and XoPPeNXiaM XentNe. it is one oI the MaNQest Xities in the ZoNMd and the MaNQest XitD in eFNoSe. its SoSFMation is aEoFt 8 PiMMion. Mondon is diYided into seYeNaM SaNts: the XitD, ZestPinsteN, the Zest end, and the east end. the heaNt oI Mondon is the XitD, its IinanXiaM and EFsiness XentNe. nFPeNoFs EanUs, oIIiXes, and IiNPs aNe sitFated theNe, inXMFdinQ the EanU oI enQMand, the stoXU eAXhanQe, and the oMd EaiMeD. IeZ SeoSMe MiYe heNe, EFt oYeN a PiMMion SeoSMe XoPe to the XitD to ZoNU. theNe aNe soPe IaPoFs anXient EFiMdinQs Zithin the XitD. SeNhaSs the Post stNiUinQ oI theP is the st. SaFM\’s XathedNaM, the QNeatest oI enQMish XhFNXhes. it Zas EFiMt in the 17th XentFND ED siN XhNistoSheN ZNen. the toZeN oI Mondon Zas IoFnded ED OFMiFs XaesaN and in 1066 NeEFiMt ED ZiMMiaP the XonTFeNoN. it Zas Fsed as a IoNtNess, a NoDaM SaMaXe, and a SNison. noZ it is a PFseFP.
Далее действуя аналогично или просто подбирая буквы по смыслу, находим исходный текст:
London is the capital of Great Britain, its political, economic, and commercial centre. It is one of the largest cities in the world and the largest city in Europe. Its population is about 8 million. London is divided into several parts: the City, Westminster, the West End, and the East End. The heart of London is the City, its financial and business centre. Numerous banks, offices, and firms are situated there, including the Bank of England, the Stock Exchange, and the Old Bailey. Few people live here, but over a million people come to the City to work. There are some famous ancient buildings within the City. Perhaps the most striking of them is the St. Paul’s Cathedral, the greatest of English churches. It was built in the 17th century by Sir Christopher Wren. The Tower of London was founded by Julius Caesar and in 1066 rebuilt by William the Conqueror. It was used as a fortress, a royal palace, and a prison. Now it is a museum.
Как видишь, в этом криптоанализе нашим главным инструментом был статистический анализ частот. Идем дальше!
Шифр Рихарда Зорге
Нельзя рассказывать о шифрах и ни слова не сказать о шпионах. В недалеком прошлом, когда компьютеров еще не было, информацию стремились скрыть в основном разведчики. Наука о шифровании не могла стоять на месте, ведь служба Родине была самым важным и нужным ее предназначением. Кстати, именно советские шифры, разработанные отечественными специалистами, на многие десятилетия вперед определили вектор развития криптографии.
Давай разберем довольно известный шифр Рихарда Зорге — советского разведчика, который был направлен в Японию. Этот шифр продуман до мелочей. Шифрование ведется на английском языке. Первоначально нужно составить следующую таблицу:
| S | U | B | W | A | Y |
| C | D | E | F | G | H |
| I | J | K | L | M | N |
| O | P | Q | R | T | V |
| X | Y | Z | . | / |
Сначала записываем в нее слово SUBWAY, выбранное нами. Затем пишем все остальные буквы алфавита по порядку. Слеш означает новое слово (разделитель), а точка обозначает себя. Далее наиболее часто встречающиеся буквы английского алфавита (A, S, I, N, T, O, E, R) нумеруются в порядке появления в таблице:
| 0) S | U | B | W | 5) A | Y |
| C | D | 3) E | F | G | H |
| 1) I | J | K | L | M | 7) N |
| 2) O | P | Q | 4) R | 6) T | V |
| X | Y | Z | . | / |
Саму таблицу мы строим по горизонтали, записывая буквы рядами, а нумеруем по вертикали, столбцами. Так улучшаются перемешивающие свойства.
Далее таблица преобразуется к следующему виду: сначала в строку по столбцам записываются наиболее часто встречаемые буквы в порядке нумерации (S, I, E, …). А затем записываются и все остальные буквы, также по столбцам в строки (С, X, U, D, J, …). Такая таблица обеспечит хорошие перемешивающие свойства и в то же время не «испортит» частотный анализ шифротекста:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| — | S | I | O | E | R | A | T | N | — | — |
| 8 | C | X | U | D | J | P | Z | B | K | Q |
| 9 | . | W | F | L | / | G | M | Y | H | V |
Таблица готова. Теперь можно зашифровать сообщение.
О безопасности
Самое уязвимое место криптографической защиты — это человек. Если браузер получил сертификат открытого ключа, проверил его цепочку сертификатов и оказалось, что он не подписан корневым доверенным центром, он покажет пользователю предупреждение, что соединение небезопасно. Что делает пользователь? — «Все равно зайти». Поэтому современные браузеры мешают проделать этот небезопасный путь и пытаются защитить пользователя от самого себя — нужно не один раз «все равно зайти», а несколько. Но если пользователь все-таки соглашается, то злоумышленник показывает страницу якобы «ВКонтакте», просит ввести его логин, пароль или номер телефона, после чего возникает экран: «Ведутся технические работы». Можно сделать хитрее и запрашивать от вашего имени у сервера страницы «ВКонтакте» и показывать их вам, пропуская через себя и читая ваш трафик так, чтобы вы ничего не заподозрили. Такая атака называется «человек посередине» или man-in-the-middle. Чтобы прочитать вашу переписку, то есть совершить атаку man-in-the-middle, нужно выдать себя за другого человека, когда связь только-только устанавливается. Происходит следующее:
1) В тот момент, когда Боб посылает свой открытый ключ серверу, Мэн перехватывает сообщение. 2) Мэн посылает свой открытый ключ серверу, выдав себя за Боба. 3) Сервер посылает свой открытый ключ лже-Бобу. Мэн посылает Бобу свой открытый ключ, выдав себя за сервер. 4) Если у Боба нет цепочки доверенных сертификатов, атака совершена.
Тем, кто работает в крупных компаниях, необходимо понимать, сколько стоит информация, ее защита, взлом защищенной системы и внедрение системы безопасности. Самый защищенный компьютер — отключенный от всех сетей, в том числе электрической, убранный в сейф (и спрятанный ключ). Поэтому любая защита — это баланс между тем, чтобы было удобно работать, и тем, чтобы система была достаточно защищена. «Достаточно» — это значит, что стоимость взлома превышает стоимость информации для злоумышленника. В крупных компаниях все это посчитано, а обычным пользователям достаточно соблюдать элементарные меры предосторожности. К сожалению, большинство пользователей не понимают, зачем вообще нужно шифрование. Серверам приходится усложнять парольную политику, но делают они это не для того, чтобы сохранить приватность вашей переписки или других данных (им это не нужно), они делают это, чтобы защититься от спама.
Криптография в XVII-XVIII веках
17 век называют эрой «черных кабинетов», поскольку в этот период создаются дешифровальные службы. Так, в Англии Оливер Кромвель создает «Интеллиженс сервис»- разведывательную службу, в которой появиться дешифровальное отделение. В середине 17 века к дешифровальной работе привлекается известный математик Джон Валлис (). Он является автором фундаментального труда «Арифметика бесконечного» (1655). Хорошо известна «формула Валлиса», дающая представление числа «пи» в виде бесконечного произведения. Во Франции при Людовике XIV по предложению кадинала Ришелье создается дешифровальное отделение, которое возглавил Антуан Россиньоль. Россиньолю принадлежит доктрина: стойкость военного шифра должна быть такой, чтобы обеспечить секретность донесения в течение срока, необходимого для выполнения приказа. Стойкость дипломатического шифра должна обеспечивать секретность в течение нескольких десятков лет. Сам Ришелье оставил след в криптографии благодаря известному «шифру Ришелье», который представляет собой шифр перестановки, при котором открытый текст разбивается на отрезки, а внутри каждого отрезка буквы переставляются в соответствии с фиксированной перестановкой.
Россиньоль разработал дипломатический шифр, представляющий собой слогово-словарный код на 600 величин.
В Германии в это время также создается дешифровальное отделение, которое возглавляет граф Гронсфельд. Ему принадлежит усовершенствование шифра Виженера, заключающееся в том, что вместо буквенного лозунга применяется цифровой, а значение цифры в лозунге означает число шагов, на которое надо сдвинуть букву открытого текста вправо по алфавиту в стандартной записи. Данный шифр получил широкое распространение благодаря простоте применения. Таким образом, дешифровальные подразделения становятся обычным делом. Что касается шифров, то в этот период применяются, в основном, коды различной степени сложности. Из других шифров следует упомянуть «массонский шифр», представляющий собой оригинальный значковый шифр, в котором из написания алфавита на двух крестах-прямом и косом извлекались знаки для замены букв. Наполеон во время своих походов использовал шифры, являющиеся вариантами шифра Россиньоля и представляющие собой код на 200 шифрвеличин.
Криптография в России развивалась по пути христианских стран. Датой появления криптографической службы следует считать 1549 год (царствование Ивана IV), с момента образования «посольского приказа», в котором имелось «цифирное отделение». Используемые шифры — такие же как в западных странах — значковые, замены, перестановки. Петр I полностью реорганизовал криптографическую службу, создав «Посольскую канцелярию». В это время применяются для шифрования коды, как приложения к «цифирным азбукам». В знаменитом «деле царевича Алексея» в обвинительных материалах фигурировали и «цифирные азбуки».
Математика 17-18 века получает существенное и качественно новое развитие. Н. Бурбаки называют этот период «героической эпохой». Назовем только некоторых авторов открытий. Изобретатель логарифмов-Дж. Непер, шотландский математик, его «Описание удивительной таблицы логарифмов» было издано в 1614 году. Декарт Рене, французский математик, заложил основы аналитической геометрии. Его фундаментальный труд «Геометрия» вышел в 1637 году.
Блез Паскаль (), французский физик и математик. Получил ряд результатов по комбинаторике («треугольник Паскаля» и геометрии («теорема Паскаля»). Открыл метод доказательства по индукции.
Ньютон Исаак() английский физик и математик и Готфрид Лейбниц ()-немецкий философ и математик разработали дифференциальное и интегральное исчисление. Не имеется данных о привлечении этих математиков к шифровальной работе, но есть данные о том, что некоторые их них владели криптографией. (Паскаль, Ньютон, Лейбниц). Увлекался криптографией и знаменитый английский философ Ф. Бекон (), которому принадлежит идея двоичного кодирования.
Якоб Бернулли (), швейцарский математик, заложил основы теории вероятностей, ему принадлежит известная теорема Бернулли, являющаяся важным частным случаем закона больших чисел. Его книга «Искусство предположений» вышла в 1713 году.
Для развития математики в России большую роль сыграла «Арифметика» , изданная в 1703 году, которую назвал «вратами учености» и представляла собой свод математических сведений на тот период.
К дешифровальной работе в России был привлечен известный математик Христиан Гольбах (), приехавший в Россию в 1725 году. В 1727 в Россию приезжает Леонард Эйлер (), который принимал участие в разработке шифров. Ему принадлежат исследования по перечислению и построению латинских квадратов, т. е. шифров многоалфавитной замены. В области математики Эйлер существенно обогатил все разделы математического анализа и заложил основы новых математических дисциплин (теория чисел, вариационное исчисление, уравнения с частными производными, теория функций комплексного переменного). Дешифровальной работой занимался Франц Эпинус (), в России с 1757 года, известный математик и физик, изучавший математическими методами электромагнитные явления.
Таким образом, в 17-18 веках в математике закладываются основы аппарата, применяемого в криптографии для анализа шифров и дешифрования.
Основным средством для шифрования становятся коды.
Big Data is watching
Для тех, кто беспокоится о приватности: поведение в интернете обрабатывается компьютером с одной единственной целью — продать вас рекламодателю. В современном мире интернет знает о вас все — пол, возраст, увлечения, профессию, даже если вы ему этого не говорили. Big Data позволяет провести анализ вашего поведения и отправить информацию о вас всем возможным рекламодателям еще до того, как вы увидели на сайте кучу баннеров. Эти данные стоят дорого, и их собирают не только чтобы настучать, а чтобы продать. От такого нарушения неприкосновенности частной жизни спасают баннерорезки или, например, Tor, который стирает личность пользователя в сети. А мессенджеры вроде Telegram или Whats Up работают на доверии пользователя к поставщику приложения, что он не воспользуется доступом к частным данным.
Криптография в XIX веке
В 1819 году во Франции выходит энциклопедия, в которой приведены известные к тому времени системы шифров и методы дешифрования простейших шифров. В 1844 году С. Морзе изобрел телеграф. В России телеграф был изобретен в 1832 году. Шиллингу также принадлежит изобретение биграммного шифра. В Англии изобретение биграммного шифра приписывается министру почт при королеве . Изобретение телеграфа оказало существенное влияние на криптографию. Сразу же был опубликован коммерческий код под названием «Словарь для тайной корреспонденции; приспособлен для применения на электромагнитном телеграфе Морзе». Развитие коммерческих кодов повлияло и на развитие дипломатических кодов. Специалисты в области шифрованной связи пришли к пониманию, что необходима иерархия в шифрованной связи. Для каждого уровня иерархии требуется своя система шифра Возрастание скорости передачи потребовало возрастание скорости шифрования. Появляются различные механические устройства для зашифрования. Среди них шифратор Т. Джеферсона и шифратор Ч. Уитстона. Устройство Уитстона демонстрировалось на парижской выставке 1876 года.
Отметим, что в викторианской Англии к дешифровальной работе был привлечен математик Ч. Беббидж, известный изобретением вычислительной машины.
В 1863 году офицер прусской армии майор Фридрих Казисский опубликовал книгу под названием «Искусство тайнописи и дешифрования», в которой новым вкладом в криптографию было изложение метода вскрытия многоалфавитного шифра с повторяющимся лозунгом на примере шифра Виженера, который ранее считался недешифруемым. Казисский предложил метод статистического определения числа букв в лозунге, который основан на следующей идее: повторяемость букв в лозунге вместе с повторяемостью букв в открытом тексте дает повторяемость букв в шифрованном тексте. Автор пришел к выводу, что расстояние между повторениями в шифртексте будут равны или кратны периоду лозунга, т. е. его длине. После определения длины лозунга шифртекст разбивается на отрезки, равные длине лозунга, и исходная задача сводится к дешифрованию простой замены. Данный метод дешифрования стал называться «методом Казисского».
В 1883 году появился крупный научный труд под названием «Военная криптография», его автор Огюст Кергоффс, преподаватель иностранных языков и математики во Франции.
В данной книге проводится сравнительный анализ шифров. Задача автора-сформулировать требования к шифрам, применительно к использованию новых средств связи. Он делает вывод, что практический интерес представляют те шифры, которые остаются стойкими при интенсивной переписке.
Другой его вывод: только криптоаналитики могут судить о качестве шифра. Кергоффс впервые делает различие между секретностью шифрсистемы и секретностью ключа. И вводит требование секретности по ключу и не требует секретности системы. Это требование сохраняет свое значение и в современной криптографии.
Важное событие в криптографии было связано с именем французского офицера Э. Базери, который отрицательно относился к официальным шифрам и предложил несколько собственных систем шифров. Одна из них — это по сути шифратор Джефферсона.
Военное руководство отказалось его использовать, сославшись на то, что нет гарантий стойкости этого шифра. В 1901 году Э. Базери издал книгу «Раскрытые секретные шифры», в которой показана возможность дешифрования «Великого шифра Россиньоля».
С 80-х годов 19 века криптография во всех ведущих государствах считается наукой и ее изучают в военных академиях. Для шифрования применяются коды с перешифровкой. Созданы и используются механические устройства для шифрования. Нет свидетельств, относящихся к данному периоду, о привлечении крупных математиков для криптографической работы.
Математика 19 века характеризуется революционными открытиями, ломающими привычные представления. В первую очередь следует назвать открытие неевклидовой геометрии. Его мемуар « О началах геометрии » был напечатан в журнале «Казанский вестник» в 1829 году. Сходные результаты были получены Я. Больяи в 1832 году. и позднее строят пример непрерывной функции, не имеющей конечной производной ни в одной точке. Но это является только началом открытий патологических явлений в математике.
Г. Кантор разработал теорию бесконечных множеств и открыл первые парадоксы теории множеств. Затем аналогичные парадоксы были открыты Бурали-Форти, Ришаром, Расселом. Сложившуюся ситуацию называют «кризисом математики». Знаменитый математик А. Пуанкаре в одном из мемуаров спрашивает: «Как интуиция может обмануть нас до такой степени?». Такое положение дел подтолкнуло к изучению оснований математики, развитию формальных языков и аксиоматического метода. Началась арифметизация математики, т. е. применялся метод, при котором рассуждение о математических объектах сводится к рассуждению о натуральных числах.
На математическом конгрессе 1900 года в Париже известный немецкий математик Д. Гильберт, формулируя актуальные проблемы математики, на место № 2 в списке проблем ставит вопрос о непротиворечивости арифметики., а на место №1 проблему Кантора о мощности континуума.
Заметим, что под №8 в списке проблем Д. Гильберта стоит проблема простых чисел, в которой, в частности, цитируется гипотеза Римана о распределении нулей дзета-функции Римана. Данная проблема, как показали современные исследования, имеет важное значение для криптографии в связи с построением алгоритмов факторизации чисел.
Что будет в 2022?
Надо понимать, что 30% трафика передаются по зашифрованному каналу — сюда входят все сообщения, картинки и так далее. Оставшиеся 70%, возможно, приходятся на видео, так как его шифровать накладно. В 2022 году вступят в силу законы, среди которых есть пункт, согласно которому операторы связи должны предоставлять весь трафик пользователя в расшифрованном виде. Но как это сделать, там не написано, и сейчас технической возможности для этого у них нет. Единственное, что есть, похоже на то, как это происходит в Казахстане. А именно, между вами и всеми сервисами — Google, Facebook, «Яндекс», «ВКонтакте», «Одноклассники», «Мой круг», Flickr, mipt.ru и так далее — операторы вставляют свой сервер, который будет выдавать себя за них с точки зрения протокола. При этом они говорят: «Чтобы пользоваться интернетом, нужно установить себе новый доверенный сертификат, это нужно для вашей же безопасности» (хотя на самом деле — чтобы оператор мог читать вашу переписку). Только в этом случае оператор получит доступ ко всем передаваемым сообщениям. Скорее всего, в 2022 году это и случится. Дальше либо запретят VPN (Virtual Private Network, виртуальная частная сеть), либо будет как в Китае, где запрещен Twitter и большинство людей защищены от информации.


Взламывать шифры — тоже наука, она называется криптоанализом. Криптология объединяет под собой науку шифрования и дешифрования. Кроме информации, можно скрыть сам факт передачи информации. Это если, например, побрить человека налысо, набить у него на голове татуировку и, когда волосы отрастут, отправить его получателю зашифрованного послания. Известным способом замаскировать зашифрованное послание под невинное письмо является решетка Кардано. Современные методы позволяют оставлять зашифрованные послания в изображениях, музыке, видео.
Не пропустите следующую лекцию:


Отвечая за судьбы мира
Актуальность криптографии резко возросла после изобретения радио. Его активно использовали для военной связи, но угроза перехвата сообщений заставляла изобретать все более сложные способы их шифрования. Во время войн XX века сражения шли не только на поле боя — криптоаналитики тоже бились на невидимом фронте, стремясь расшифровать перехваченные радиограммы и заранее узнавать о готовящихся действиях противника.


Коммутационная панель в передней части «Энигмы»
Была в этом и обратная сторона: если вражеское командование видело, что его планы оказались раскрыты, оно меняло ключ или даже всю систему шифрования. Сколько займет вскрытие нового шифра и состоится ли оно вообще, заранее не знал никто. Поэтому порой приходилось имитировать неведение и даже идти на жертвы, чтобы противник и дальше продолжал применять скомпрометированный шифр. Многие убеждены, что Черчилль пожертвовал английским Ковентри — позволил обстрелять город, лишь бы немцы не догадались, что секрет их легендарной «Энигмы» (одной из самых известных шифровальных машин Второй мировой войны) уже раскрыт. Вероятно, это была большая тактическая уступка ради сохранения выигрышной стратегии.