- Введение
- Объекты и их признаки
- Обучение с учителем
- Нейрон
- Сеть нейронов
- Нейрон как гиперплоскость
- Уверенность нейрона
- Полезность нейрона
- Несколько выходов
- Когда нужен скрытый слой
- Нейроны как логические элементы
- Четыре варианта xor
- Аппроксимация функции y=f(x)
- Аппроксимация функции на Phyton
- Нечёткая логика
Введение
Этим документом начинается серия материалов, посвящённых нейронным сетям. Иногда к ним относятся по принципу: человеческая нейронная сеть может решать любые задачи, поэтому и достаточно большая искусственная нейронная сеть на это способна. Чаще всего архитектура сети и параметры её обучения являются предметом многочисленных экспериментов. Сеть при этом оказывается чёрным ящиком, происходящее в котором загадочно даже для её учителя.
Мы постараемся совмещать эмпирические советы и математическое понимания природы нейронов как разделяющих гиперплоскостей и функций нечёткой логики. Сначала будут рассмотрены различные модельные примеры двумерных пространств признаков. Наша цель — выработать интуитивное понимание выбора архитектуры сети. В дальнейшем мы перейдём к многомерным задачам, распознанию графических образов, свёрточным и рекуррентным сетям. Приведенные ниже примеры можно запустить, потренировавшись в подборе параметров обучения.
Optimizers
Оптимизаторы — очень важная вещь, потому что это функция, которая помогает нейронной сети изменять веса при обратном распространении, так что разница между фактическим и прогнозируемым результатом будет постепенно уменьшаться и достигать точки, в которой потери очень минимальны и модель способна предсказывать более точные результаты.
Опять же, TensorFlow поддерживает множество оптимизаторов, чтобы упомянуть несколько,
- Gradient descent
- SDG – Stochastic Gradient Descent
- Adagrad
- Adam
После компиляции модели нам нужно подогнать модель к набору данных для обучения,
Python
# fitting the model
model.fit(train_data, train_label,
epochs=5, batch_size=32)
Объекты и их признаки
Пусть есть однотипные объекты
(бутылки с вином, посетители в больнице, позиции на шахматной доске):
Каждый объект характеризуется набором (вектором) признаков
x={x1,x2,…,xn}
. Признаки могут быть:
- вещественными (вес, рост)
- бинарными (женщина/мужчина)
- нечисловыми (красный,синий,…)
Далее будем считать признаки вещественными числами из диапазона [0…1]
. Этого всегда можно достичь при помощи нормировки, например:
x -> (x-xmin)/(xmax-xmin)
. Бинарные признаки, соответственно, принимают значение
0
или
1
. Нечисловые признаки, увеличив размерность вектора
x
, можно сделать бинарными (красный/не красный, синий/не синий). Кроме этого, пока будем считать, что объекты между собой причинно не связаны и их порядок не существенен.
Пусть объекты данного типа разбиваются на классы (человек: {здоровый, больной}, вино: {итальянское, французское, грузинское}). С каждым объектом можно также связать некоторое число y
(степень преимущества белых в шахматной позиции; качество вина по усреднённому мнению экспертов и т.д.). Часто решаются следующие две, тесно связанные задачи:
- Классификация:
к какому из
K
классов принадлежит объект. - Регрессия:
какое число
y
соответствует объекту.
Примеры:
- 1) 3 признака: x
={температура, уровень гемоглобина, количество холестерина}; 2 класса: {
0
: здоровый,
1
: больной}; - 2) w*h
признаков:
x
={яркости пикселей картинки шириной
w
и высотой
h
}; 10 классов: {
0-9
: цифра на картинке}. - 3) 8*8*13
признаков:
x
={коды шахматных фигур в ячейках}; регрессия: {преимущество белых на чёрными =
[-1…1]
}.
Для успешного решения задач классификации или регрессии, признаки, характеризующие объект, должны быть значимыми, а вектор признаков — полным (достаточным для классификации объектов или определение регрессионной величины y
).
Однажды Джед и Нед захотели различать своих лошадей. Джед сделал на ухе лошади царапину. Но лошадь Неда поцарапала о колючку тоже самое ухо. Тогда Нед прицепил голубой бант на хвост своей лошади, но лошадь Джеда его сожрала. Фермеры долго размышляли и выбрали признак, который не так легко изменить. Они тщательно измерил высоту лошадей, и оказалось, что черная кобыла Джеда на один сантиметр выше белого жеребца Неда.
Обучение с учителем
Пусть есть множество объектов, каждый из которых принадлежит одному из k
пронумерованных
(0,1,2,…k-1)
классов. На этом
обучающем множестве
, предоставленнным «учителем» (обычно человеком), система обучается. Затем, для неизвестных системе объектов (
тестовом множестве
), она проводит их классификацию, т.е. сообщает к какому классу принадлежит данный объект. В такой постановке — это задача распознавания образов после обучения с учителем.
Число признаков n
называется
размерностью пространства признаков
. Пусть признаки лежат в диапазоне
[0…1]
. Тогда любой объект представим точкой внутри единичного
n
-мерного куба в пространстве признаков.
Распознающую систему представим в виде чёрного ящика. У этого ящика есть n
входов, на которые подаются значения признаков
x={x1,x2,…,xn}
и
k
выходов
y={y1,…,yk}
(по числу классов). Значение выходов также будем считать вещественным числами из диапазона
[0…1]
. Система считается правильно обученной, если при подаче на входы признаков, соответствующих
i
-тому классу, значение
i
-того выхода равно
1
, а всех остальных
0
. На практике, такого результата добиться трудно и все выходы оказываются отличными от нуля. Тогда считается что номер выхода с максимальным значением и есть номер класса, а близость этого значения к единице говорит о «степени уверенности» системы.
Когда есть только два класса, ящик может иметь один выход. Если он равен 0
, то это один класс, а если
1
— то другой. При нечётком распознавании вводятся пороги уверенности. Например, если значение выхода лежит в диапазоне
y=[0 … 0.3]
— это первый класс, если
y=[0.7 … 1]
— второй, а при
y=(0.3 … 0.7)
система «отказывается принимать решение».
Ящик с одним выходом может также аппроксимировать функцию y=f(x1,…,xn)
, значения
y
которой непрерывны и обычно также нормируются на единицу, т.е.
y=[0 … 1]
. В этом случае решается задача регрессии.
Обучение нейронной сети
Теперь давайте чуть более подробно рассмотрим вопрос обучения нейронной сети. Что это такое? И каким образом это происходит?
Что такое обучение сети?
Искусственная нейронная сеть – это совокупность искусственных нейронов. Теперь давайте возьмем, например, 100 нейронов и соединим их друг с другом. Ясно, что при подаче сигнала на вход, мы получим что-то бессмысленное на выходе.
Значит нам надо менять какие-то параметры сети до тех пор, пока входной сигнал не преобразуется в нужный нам выходной.
Что мы можем менять в нейронной сети?
Изменять общее количество искусственных нейронов бессмысленно по двум причинам. Во-первых, увеличение количества вычислительных элементов в целом лишь делает систему тяжеловеснее и избыточнее. Во-вторых, если вы соберете 1000 дураков вместо 100, то они все-равно не смогут правильно ответить на вопрос.
Сумматор изменить не получится, так как он выполняет одну жестко заданную функцию – складывать. Если мы его заменим на что-то или вообще уберем, то это вообще уже не будет искусственным нейроном.
Если менять у каждого нейрона функцию активации, то мы получим слишком разношерстную и неконтролируемую нейронную сеть. К тому же, в большинстве случаев нейроны в нейронных сетях одного типа. То есть они все имеют одну и ту же функцию активации.
Остается только один вариант – менять веса связей.
Обучение нейронной сети (Training) — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.
Такой подход к термину «обучение нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей. Каждая из них в отдельности состоит из нейронов одного типа (функция активации одинаковая). Мы обучаемся благодаря изменению синапсов – элементов, которые усиливают/ослабляют входной сигнал.
Однако есть еще один важный момент. Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ». Со стороны будет казаться, что она очень быстро «обучилась». И как только вы подадите немного измененный сигнал, ожидая увидеть правильный ответ, то сеть выдаст бессмыслицу.
В самом деле, зачем нам сеть, определяющая лицо только на одном фото. Мы ждем от сети способности обобщать какие-то признаки и узнавать лица и на других фотографиях тоже.
Именно с этой целью и создаются обучающие выборки.
Обучающая выборка (Training set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.
После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике.
Однако прежде чем пускать свежеиспеченную нейросеть в бой, часто производят оценку качества ее работы на так называемой тестовой выборке.
Тестовая выборка (Testing set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.
Мы поняли, что такое «обучение сети» – подбор правильного набора весов. Теперь возникает вопрос – а как можно обучать сеть? В самом общем случае есть два подхода, приводящие к разным результатам: обучение с учителем и обучение без учителя.
Обучение с учителем
Суть данного подхода заключается в том, что вы даете на вход сигнал, смотрите на ответ сети, а затем сравниваете его с уже готовым, правильным ответом.
Важный момент. Не путайте правильные ответы и известный алгоритм решения! Вы можете обвести пальцем лицо на фото (правильный ответ), но не сможете сказать, как это сделали (известный алгоритм). Тут такая же ситуация.
Затем, с помощью специальных алгоритмов, вы меняете веса связей нейронной сети и снова даете ей входной сигнал. Сравниваете ее ответ с правильным и повторяете этот процесс до тех пор, пока сеть не начнет отвечать с приемлемой точностью (как я говорил в 1 главе, однозначно точных ответов сеть давать не может).
Обучение с учителем (Supervised learning) — вид обучения сети, при котором ее веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов.
Где взять правильные ответы?
Если мы хотим, чтобы сеть узнавала лица, мы можем создать обучающую выборку на 1000 фотографий (входные сигналы) и самостоятельно выделить на ней лица (правильные ответы).
Если мы хотим, чтобы сеть прогнозировала рост/падение цен, то обучающую выборку надо делать, основываясь на прошлых данных. В качестве входных сигналов можно брать определенные дни, общее состояние рынка и другие параметры. А в качестве правильных ответов – рост и падение цены в те дни.
И так далее…
Стоит отметить, что учитель, конечно же, не обязательно человек. Дело в том, что порой сеть приходится тренировать часами и днями, совершая тысячи и десятки тысяч попыток. В 99% случаев эту роль выполняет компьютер, а точнее, специальная компьютерная программа.
Обучение без учителя
Обучение без учителя применяют тогда, когда у нас нет правильных ответов на входные сигналы. В этом случае вся обучающая выборка состоит из набора входных сигналов.
Что же происходит при таком обучении сети? Оказывается, что при таком «обучении» сеть начинает выделять классы подаваемых на вход сигналов. Короче говоря – сеть начинает кластеризацию.
Например, вы демонстрируете сети конфеты, пирожные и торты. Вы никак не регулируете работу сети. Вы просто подаете на ее входы данные о данном объекте. Со временем сеть начнет выдавать сигналы трех разных типов, которые и отвечают за объекты на входе.
Обучение без учителя (Unsupervised learning) — вид обучения сети, при котором сеть самостоятельно классифицирует входные сигналы. Правильные (эталонные) выходные сигналы не демонстрируются.
Нейрон
Нейронная сеть — одно из возможных наполнений чёрного ящика. Узел сети — это нейрон, имеющий n
входов
x={x1,x2,…,xn}
и один выход
y
. С каждым входом связан вещественный параметр
синаптического весаω={w1,w2,…,wn}
. Кроме этого, нейрон имеет также «
параметр смещения
«
w0
. Таким образом, любой нейрон с
n
входами полностью определяется
n+1
параметром.
Выход нейрона вычисляется следующим образом. Значение каждого входа xi
умножают на соответствующий ему синаптический вес
wi
и эти произведения складывают. К сумме добавляют параметр смещения
w0
. Результат
d
приводят к диапазону
[0 … 1]
при помощи нелинейной
сигмоидной функцииy=S(d)
:
d = w0 + w1x1 + … + wnxn, y = S(d) = 1/(1+exp(-d)).
Сигмоидная функция стремится к 1
при больших положительных
d
и к
0
при больших отрицательных
d
. Когда
d=0
, она равна
S(0)=0.5
. Таким образом, нейрон это нелинейная функция
n
переменных порогового вида:
Epochs
Эпохи — это просто количество раз, когда весь набор данных проходит вперед и назад путем обновления весов в нейронной сети. Делая это, мы можем находить невидимые закономерности и информацию для каждой отдельной эпохи, и, следовательно, это повышает точность модели.
И чтобы справиться с некоторыми ограничениями нейронных сетей, такими как переоснащение обучающих данных и невозможность хорошо работать с невидимыми данными. Это может быть решено с помощью некоторых выпадающих слоев, что означает, что некоторое количество узлов в слое становится неактивным, что заставляет каждый узел в нейронной сети узнавать больше об особенностях ввода, и, следовательно, проблема может быть решена.
Сеть нейронов
Сеть является множеством соединённых между собой нейронов. Возможны различные способы соединения и, следовательно, различные архитектуры сети. Пусть нейроны располагаются слоями и значения выходов нейронов i
-того слоя подаётся на входы всех нейронов следующего
i+1
слоя. Такую сеть называют полносвязной сетью прямого распространения. Входы сети мы будем обозначать квадратиками и называть входными нейронами. В отличии от «обычных» нейронов — это просто линейная функция
y=x
. Выходы нейронов последнего слоя сети являются выходами чёрного ящика и обозначаются треугольниками.
Ниже на первом рисунке сеть состоит из трёх входов (нулевой слой) и двух выходных нейронов. Такую архитектуру будем кодировать следующим образом: [3,2]
, где цифры — это число нейронов в слое. Первая цифра — всегда количество входов, а последняя — количество выходов. На следующем рисунке представлена сеть
[2,3,1]
. Она содержит один
скрытый слой
с тремя нейронами. Он скрыт в том смысле, что находится внутри чёрного ящика (пунктир) между входным и выходным слоем (нейроны выходного слоя, впрочем, также частично скрыты и наружу «торчат» только их выходы). На третьем рисунке представлена сеть
[2,3,3,2]
с двумя скрытыми слоями.
Эти сети названы сетями прямого распространения потому, что данные (признаки объекта) подаются на вход и последовательно, без петель, передаются (распространяются) к выходам. К такому же типу сетей относятся т.н. свёрточные сети
, в которых соединены между собой не все нейроны двух соседних слоёв (ниже первый рисунок). Часто при этом веса у всех нейронов свёрточного слоя одинаковые. Подробнее о таких сетях будет говориться при распознавании изображений. На втором рисунке ниже представлен вариант сети в которой понятие слоя отсутствует, однако это по-прежнему сеть прямого распространения.
Последний рисунок — это уже сеть не прямого распространения, а т.н. рекуррентная сеть
. В ней сигналы с одного или нескольких выходных нейронов подаются обратно на вход. Обычно такая рекурсия, проводится в несколько циклов, пока на выходах сети не установятся стационарные значения. Рекуррентные сети обладают памятью и последовательность подачи объектов для них важна. Такое поведение полезно, если объекты упорядочены во времени (например при предсказании временных рядов).
Обучение любой сети состоит в подборе параметров w0,w1,…,wn
каждого нейрона, таким образом, чтобы для данного объекта (подаём на входы сети
x1,…,xn
), выходы сети имели значения, соответствующие классу объекта.
Отметим, что, хотя нейрон всегда имеет только один выход, он может «подаваться» на входы различных нейронов. Аналогично, в живых нейронах аксон расщепляется на отдельные отростки, каждый их которых воздействует на синапсы («точки соединения») дендридов других нейронов. Если нейрон возбудился, то это возбуждение передаётся по аксону к дендридам его соседей.
Искусственный нейрон
Теперь мы переходим к рассмотрению внутренней структуры искусственного нейрона и того, как он преобразует поступающий на его входы сигнал.
На рисунке ниже представлена полная модель искусственного нейрона.
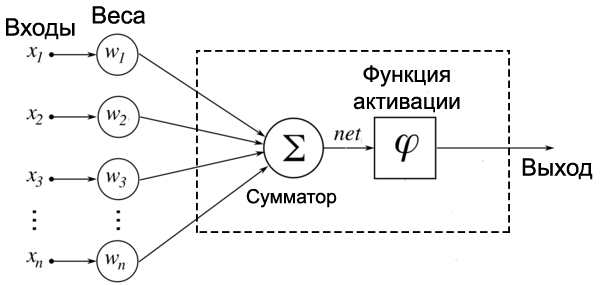
Не пугайтесь, ничего сложного здесь нет. Давайте рассмотрим все подробно слева направо.
Входы, веса и сумматор
У каждого нейрона, в том числе и у искусственного, должны быть какие-то входы, через которые он принимает сигнал. Мы уже вводили понятие весов, на которые умножаются сигналы, проходящие по связи. На картинке выше веса изображены кружками.
Поступившие на входы сигналы умножаются на свои веса. Сигнал первого входа \( x_1 \) умножается на соответствующий этому входу вес \( w_1 \). В итоге получаем \( x_1w_1 \). И так до \( n \)-ого входа. В итоге на последнем входе получаем \( x_nw_n \).
Теперь все произведения передаются в сумматор. Уже исходя из его названия можно понять, что он делает. Он просто суммирует все входные сигналы, умноженные на соответствующие веса:
\[ x_1w_1+x_2w_2+\cdots+x_nw_n = \sum\limits^n_{i=1}x_iw_i \]
Математическая справка
Сигма – Википедия Когда необходимо коротко записать большое выражение, состоящее из суммы повторяющихся/однотипных членов, то используют знак сигмы.
Рассмотрим простейший вариант записи:
\[ \sum\limits^5_{i=1}i=1+2+3+4+5 \]
Таким образом снизу сигмы мы присваиваем переменной-счетчику \( i \) стартовое значение, которое будет увеличиваться, пока не дойдет до верхней границы (в примере выше это 5).
Верхняя граница может быть и переменной. Приведу пример такого случая.
Пусть у нас есть \( n \) магазинов. У каждого магазина есть свой номер: от 1 до \( n \). Каждый магазин приносит прибыль. Возьмем какой-то (неважно, какой) \( i \)-ый магазин. Прибыль от него равна \( p_i \).
Если мы хотим посчитать общую прибыль от всех магазинов (обозначим ее за \( P \)), то нам пришлось бы писать длинную сумму:
\[ P = p_1+p_2+\cdots+p_i+\cdots+p_n \]
Как видно, все члены этой суммы однотипны. Тогда их можно коротко записать следующим образом:
\[ P=\sum\limits^n_{i=1}p_i \]
Словами: «Просуммируй прибыли всех магазинов, начиная с первого и заканчивая \( n \)-ым». В виде формулы это гораздо проще, удобнее и красивее.
Результатом работы сумматора является число, называемое взвешенной суммой.
Взвешенная сумма (Weighted sum) (\( net \)) — сумма входных сигналов, умноженных на соответствующие им веса. \[ net=\sum\limits^n_{i=1}x_iw_i \]
Роль сумматора очевидна – он агрегирует все входные сигналы (которых может быть много) в какое-то одно число – взвешенную сумму, которая характеризует поступивший на нейрон сигнал в целом. Еще взвешенную сумму можно представить как степень общего возбуждения нейрона.
Пример
Для понимания роли последнего компонента искусственного нейрона – функции активации – я приведу аналогию.
Давайте рассмотрим один искусственный нейрон. Его задача – решить, ехать ли отдыхать на море. Для этого на его входы мы подаем различные данные. Пусть у нашего нейрона будет 4 входа:
- Стоимость поездки
- Какая на море погода
- Текущая обстановка с работой
- Будет ли на пляже закусочная
Все эти параметры будем характеризовать 0 или 1. Соответственно, если погода на море хорошая, то на этот вход подаем 1. И так со всеми остальными параметрами.
Если у нейрона есть четыре входа, то должно быть и четыре весовых коэффициента. В нашем примере весовые коэффициенты можно представить как показатели важности каждого входа, влияющие на общее решение нейрона. Веса входов распределим следующим образом:
- 5
- 4
- 1
- 1
Нетрудно заметить, что очень большую роль играют факторы стоимости и погоды на море (первые два входа). Они же и будут играть решающую роль при принятии нейроном решения.
Пусть на входы нашего нейрона мы подаем следующие сигналы:
- 1
- 0
- 0
- 1
Умножаем веса входов на сигналы соответствующих входов:
- 5
- 0
- 0
- 1
Взвешенная сумма для такого набора входных сигналов равна 6:
\[ net=\sum\limits^4_{i=1}x_iw_i = 5 + 0 + 0 + 1 =6 \]
Все классно, но что делать дальше? Как нейрон должен решить, ехать на море или нет? Очевидно, нам нужно как-то преобразовать нашу взвешенную сумму и получить ответ.
Вот на сцену выходит функция активации.
Нейрон как гиперплоскость
Чтобы чёрный ящик распознающей системы сделать прозрачнее, рассмотрим геометрическую интерпретацию нейрона. В n
-мерном пространстве каждая точка задаётся
n
координатами (вещественными числами
x= {x1,…,xn}
). Плоскость (как и в обычном 3-мерном пространстве) задаётся вектором нормали
ω={w1,…,wn}
(перпендикуляр к плоскости) и произвольной точкой
x0={x01,…,x0n}
, лежащей в этой плоскости. Когда
n > 3
плоскость принято называть
гиперплоскостью
.
Расстояние d
от гиперплоскости до некоторой точки
x={x1,…,xn}
вычисляется по формуле
d = w0 + w1 x1 + … + wn xn,
где
w0 = -(w1 x01 + … + wn x0n).
При этом d > 0
, если точка
x
лежит с той стороны плоскости, куда указывает вектор
ω
и
d < 0
, если с противоположной. Когда
d = 0
— точка
x
лежит в плоскости. Это ключевое для дальнейшего изложения утверждение, которое стоит запомнить.
Изменение параметра w0
сдвигает плоскость параллельным образом в пространстве. Если
w0
уменьшается, то плоскость смещается в направлении вектора
ω
(расстояние меньше), а если
w0
увеличивается — плоскость смещается против вектора
ω
. Это непосредственно следует из приведенной выше формулы.
◄ Вывод этой формулы (который можно пропустить) проведём в векторных обозначениях. Запишем вектор x — x0
, начинающийся в точке
x0
(лежащей в плоскости) и направленный в точку
x
(см. рисунок справа; векторы складываются по правилу треугольника). Положение точки
x0
выбрано в основании вектора
ω
, поэтому
ω
и
x — x0
коллинеарны (лежат на одной прямой). Если вектор
ω
единичный (
ω
2=1), то скалярное произведение векторов
x — x0
и
ω
равно расстоянию точки
x
до плоскости:
d = w·(x-x0) = -w·x0 + w·x = w0 + w·x.
Если длина
w=|ω
| вектора
ω
нормали к плоскости отлична от единицы, то
d
в
w
раз больше (
w>1
) или меньше (
w<1
) евклидового расстояния в
n
-мерном пространстве. Когда векторы
x — x0
и
ω
направлены в противоположные стороны:
d < 0
. ►
Если пространство имеет n
измерений, то гиперплоскость это
(n-1)
-мерный объект. Она делит всё пространство на две части. Для наглядности рассмотрим 2-мерное пространство. Гиперплоскостью в нём будет прямая линия (одномерный объект). Справа на рисунке кружок изображает одну точку пространства, а крестик — другую. Они расположены по разные стороны от линии (гиперплоскости). Если длина вектора
ω
много больше единицы, то и расстояния
d
от точек к плоскости по модулю будут существенно большими единицы.
Вернёмся к нейрону. Несложно видеть, что он вычисляет расстояние d
от точки с координатами
x=(x1,…,xn)
(вектор входов) до гиперплоскости (
w0
,
ω
). Параметры нейрона
ω=(w1,…,wn)
определяют направление нормали гиперплоскости, а
w0
связан со смещение плоскости вдоль вектора
ω
. На выход нейрона подаётся нормированное на диапазон
[0…1]
расстояние
S(d)
. При больших
wi
объект, нарисованный выше кружком, приведёт к выходу нейрона близкому к единице, а крестик — к нулю. Отношение
w0/
|
ω
| равно расстоянию от плоскости до начала координат
(0,…,0)
. По модулю оно не должно превышать
n½
1. Нейрон является гиперплоскостью. Значение его выхода равно нормированному расстоянию от вектора входов до гиперплоскости. В процессе обучения, плоскость каждого нейрона меняет свою ориентацию и сдвигается в пространстве признаков.
Уверенность нейрона
При обучении сети необходим критерий, в соответствии с которым подбираются параметры нейронов. Обычно для этого служит квадрат отклонения выходов сети от их целевых значений. Так, для двух классов и одного выхода, ошибкой Error
сети считаем
Error2 = (1/N) ∑ (y-yc)2
,
где y
— фактический выход, а
yc
— его правильное значение, равное
0
для одного класса и
1
— для второго. Сумма ведётся по
N
обучающим примерам. Эту
среднеквадратичную ошибку
по всем обучающим объектам стараются сделать минимальной. Методы минимизации ошибки (подбор параметров нейронов) мы обсудим позднее.
Рассмотрим 2-мерное пространство признаков x1,x2
и два класса
0
и
1
. На рисунке ниже объекты одного класса представлены синими кружочками, а объекты второго класса — красными крестиками. Справа от пространства признаков приведена сеть
[2,1]
из одного нейрона. За ней, на сине-красном квадратике, нарисована
карта значений
выхода нейрона при тех или иных входах (
x1,x2
пробегают значения от
0
до
1
с шагом
0.01
). Если
y=0
— то это синий цвет, если
y=1
— то красный, а белый цвет соответствует значению
y=0.5
:
σ=0.2D
Справа от рисунков под чертой, в квадратных скобках даны параметры нейрона: [w0,w1,w2]
. В круглых скобках приведена длина
|w|
вектора нормали
ω
и среднее значение выхода и его волатильность
σy
(см. ниже). Ось
x1
пространства признаков направлена вправо, а ось
x2
— вниз. Поэтому вектор
ω
с положительными компонентами
{w1, w2}
направлен по диагонали вниз (он нарисован рядом с кружочком на прямой, содержащим номер нейрона
1
).
Над чертой в таблице приведена среднеквадратичная ошибка Error
такой сети. При этом строка
Learn
означает обучающую последовательность объектов, а
Test
— проверочную, которая не участвовала в обучении (тестовые объекты на графике пространства признаков изображены полупрозрачными). Колонка
Miss
содержит процент неправильно распознанных сетью объектов (отнесённых не к своему классу). Последняя строка
kNear
означает ошибку и процент ошибок в методе
10
ближайших соседей (он будет описан позднее).
В этом примере разброс признаков объектов каждого класса невелик. Классы легко разделяются гиперплоскостью (линией в 2-мерии). Сеть стремиться минимизировать ошибку к целевым значениям 0
или
1
на выходе, поэтому модуль вектора
|
w|=48 принимает сравнительно большое значение. В результате, даже недалеко расположенные от плоскости объекты (в обычном евклидовом смысле) получают большое по модулю значение
d
. Соответственно
y=S(d) = 0
или
1
. Такой нейрон мы будем называть
уверенным
. Чем больше
|
w|, тем более уверен в себе нейрон. На его карте выхода тонкая белая линия (область неуверенности) отделяет насыщенный синий цвет (один класс) от насыщенного красного цвета (второй класс).
Несколько иная ситуация во втором примере, где существует широкая область перекрытия объектов различных классов. Теперь нейрон не столь уверен в себе и длина вектора |
w|=24 в 2 раза меньше:
σ=Dσ=D
Приведём функции деформации расстояния (сигмоид) при длине вектора нормали, равной 1,2,5,10,100
:
Так как входы нейрона нормированы на единицу, максимальное расстояние от точки x
с координатами
{x1,…,xn}
в
n
-мерном кубе (его диагональ) равна корню из
n
. В 2-мерном пространстве признаков
dmax=1.4
. Если плоскость проходит через середину куба
dmax~0.5
.
Уверенный нейрон — не всегда хороший нейрон. Если размерность пространства признаков n
велика, а обучающих данных
N
мало, сеть состоящая из уверенных нейронов может оказаться
переобученной
и на тестовых объектах приводить к большой ошибке распознавания. Кроме этого самоуверенные нейроны медленнее обучаются. Подробнее мы остановимся на этих вопросах ниже.
В заключение сформулируем главный вывод, справедливый для пространств любой размерности:
2. Если два класса в пространстве признаков разделяются гиперплоскостью, то для их распознавания достаточно одного нейрона.
Activation function
Функции активации — это просто математические методы, которые переводят все значения в диапазон от 0 до 1, так что машине будет очень легче изучить данные в процессе их анализа. Поток Tensor поддерживает множество функций активации. Некоторые из наиболее часто используемых функций:
- Sigmoid
- Relu
- Softmax
- Swish
- Linear
Каждая функция активации имеет свои конкретные варианты использования и недостатки. Но функция активации, которая используется в скрытом и входном слоях, — это «Relu», а другая функция, которая будет иметь большее влияние на результат, — это потери.
После этого мы можем увидеть параметры в компиляции модели в TensorFlow,
Python
# Compilation of model
model.compile(optimizer=’adam’
loss=a_loss_function
metrics=[‘metrics’])
Полезность нейрона
В случае, если гиперплоскость нейрона не пересекает единичный гиперкуб в котором находятся признаки (или значения выходов предыдущих нейронов), то от такого нейрона обычно мало пользы. Он не разделяет на две части входные данные (которые всегда принадлежат интервалу [0 … 1]
. Такой нейрон будет называться
бесполезным
.
Необходимо стремиться к тому, чтобы все нейроны сети были полезными. Иногда бесполезность появляется и для плоскости, пересекающей гиперкуб, если объекты любых классов оказываются с одной стороны этой плоскости.
Перед началом обучения параметры нейронов полагают равными случайным значениям. При этом нейрон может сразу оказаться бесполезным. Чтобы этого не произошло, можно использовать следующий алгоритм инициализации:
Компоненты вектора ω
задаём случайным образом, например в диапазоне
[-w … w]
, где
w ~ 1 — 10
. Затем, внутри единичного гиперкуба (или в некоторой его центральной части), выбираем случайную точку
x0={x01,…,x0n}
. Параметр сдвига задаём следующим образом:
w0 = —
ω·x0 = -(w1x01 + … + wnx0n). В результате гиперплоскость будет гарантированно проходить через гиперкуб.
Параметр сдвига стоит контролировать и в процессе обучения, так чтобы нейрон был всё время полезным. Здесь возможны два способа — геометрический и эмпирический. В эмпирическом вычисляется среднее значение выхода каждого нейрона по обучающим объектам. Если после прохождения через сеть всех обучающих примеров, средние значения некоторых нейронов близки к нулю или единице, то они считаются бесполезными. В этом случае их можно «встряхнуть» случайным образом (возможно с сохранением вектора ω
, изменяя только параметр сдвига
w0
).
На всех примерах в этом документе нейроны в сетях разукрашены в соответствии со значением их . Если = 0.5
, то нейрон белый, если
= 0
— синий, а если
= 1
— красный. Насыщенный синий или красный цвета означают бесполезность нейрона. В первых двух примерах, единственный нейрон получился очень полезным (белым), так как объекты классов равновероятно находились справа и слева от линии (разделяющей гиперплоскости).
Кроме среднего значения выхода, важную роль играет волатильность нейрона
σy, равная среднеквадратичным отклонениям его выхода от среднего значения . Чем волатильность меньше, тем менее полезен нейрон. Действительно, в этом случае, не зависимо от значений входов, он принимает одно и то же значение на выходе. Поэтому, без изменения выходных значений сети, такой нейрон можно выбросить, сдвинув соответствующим образом параметры нейронов, для которых бесполезный нейрон является входным.
Перспективы и реальность
Сейчас уже создано много эффективных и перспективных проектов с внедрением нейронных сетей в медицину — гораздо больше, чем описано здесь. Пока внедрение происходит медленно; требуется больше данных, чтобы приобрести уверенность в эффективности нейросетей и в том, что нейронные сети не будут делать роковых ошибок. Кроме того, внедрение нейросетей потребует изменения алгоритма работы медучреждений. Дополнительной проблемой является то, что по сути мы не можем узнать точно, как именно нейронная сеть пришла к выводу, поскольку скрытый слой, хоть его и настраивают люди, представляет из себя черный ящик, тогда как врач всегда может рассказать, почему он поставил такой диагноз. Нейронным сетям будет сложно доверять — мало ли что они там решили?
Тем не менее, возможности нейронных сетей очень велики, и если все сложится удачно, они станут превосходными помощниками врачей, смогут выполнять за них многие задачи, выступать в роли второго мнения в сложных случаях. В перспективе нейросети сделают диагностику гораздо более быстрой и эффективной, а мониторинг заболеваний будет возможен в домашних условиях. Они смогут сделать жизнь проще и врачам, и пациентам.
Несколько выходов
Рассмотрим теперь 3
класса. Использовать один нейрон не очень удобно, поэтому, как было описано в начале документа, создадим сеть
[2,3]
с тремя выходами. Пусть классы локализованы в пространстве признаков следующим образом:
Каждый выходной нейрон отделяет «свой класс» от остальных двух. Например, первый сверху нейрон (на рисунке горизонтальная плоскость номер 1
) распознаёт объекты, помеченные синими кружочками, выдавая на выходе
1
, если объект находится с той стороны, куда направлен вектор
ω
(чёрточка рядом с номером плоскости).
Аналогично, второй нейрон распознаёт красные крестики, а третий — зелёные квадратики. В каждом случае векторы нормали направлены в сторону «своих» классов. Все нейроны сети достаточно уверенны в себе и вполне полезны. Их небольшая синева связана с тем, что против вектора нормали всегда расположено вдвое больше данных («чужих» двух классов), чем по вектору. Поэтому среднее значение каждого выхода смещено ниже нейтрального уровня 0.5
.
Когда нужен скрытый слой
Перейдём теперь к чуть более сложной задаче. Пусть объекты двух классов (кружочки и крестики) сосредоточены по углам пространства признаков так, как на рисунке справа. Одной гиперплоскостью (линией) эти два класса разделить нельзя. Иногда такую задачу называют разделяющим ИЛИ (xor
). Эта логическая операция равна истине (единице) только, если один из аргументов равен истине, а второй лжи (нулю): «Маша любит или Колю или Васю, но не их обоих». На рисунке классу, помеченными кружками, на выходе сеть должна выдавать ноль, а классу крестика — единицу. Если объекты находятся точно в углах, то
xor(0,0) = xor(1,1) = 0
и
xor(0,1) = xor(1,0) = 1
.
Чтобы провести классификацию, необходима нейронная сеть [2,2,1]
с одним скрытым слоем. Ниже на первом графике (в осях признаков
x1
и
x2
) показаны две гиперплоскости (линии
A
и
B
). Они соответствуют двум скрытым нейронам
A
и
B
. Значения выходов нейронов приведены на втором графике (оси
yA
и
yB
).
Оба крестика лежат по направлениям векторов нормалей плоскостей A
и
B
. Поэтому расстояние от них к плоскостям будет положительным и, если нейроны достаточно уверены в себе, на их выходах
yA
и
yB
будет получаться единица (нижний правый угол плоскости
yA
,
yB
).
Кружок с признаками (0,0)
из верхнего левого угла плоскости
x1
,
x2
даст на выходах нейронов
yA~0
,
yB~1
(этот объект лежит против вектора нормали плоскости
A
и по вектору нормали плоскости
B
). Второй кружок с признаками
(1,1)
даст на выходах нейронов значения
yA~1
,
yB~0
. Получившееся «деформированное» пространство признаков
yA
и
yB
(второй график) уже легко разделить одной плоскостью
C
, которая и будет выходным нейроном сети. Если вектор её нормали направлен так как указано на втором графике, то для обоих крестиков получится
y~1
, а для кружков
y~0
.
Ниже приведен реальный пример нейронной сети, обученной распознавать два класса объектов, каждый из которых разбивается на два кластера:
3. Каждый слой сети преобразует входное пространство признаков в некоторое другое пространство, возможно, с иной размерностью. Такое нелинейное преобразование происходит до тех пор, пока классы не оказываются линейно разделимыми нейронами выходного слоя.
Нейросети — это просто
Содержание
- Введение
- 1. Принципы построения искусственных нейронных сетей
- 2. Как устроен искусственный нейрон
- 3. Обучение сети
- 4. Строим свою нейронную сеть средствами MQL
- 4.1. Связи
- 4.2. Нейрон
- 4.3. Нейронная сеть
Введение
Все большие аспекты нашей жизнедеятельности охватывает искусственный интеллект. Все чаще новостные ленты пестрят сообщениями «нейросеть научили …» И каждый раз, когда речь заходит об искусственном интеллекте, мы рисуем в своей голове какие-то фантастические образы. Кажется, что это что-то сложное, сверхъестественное и необъяснимое. И создание такого чуда под силу только большой группе ученных мужей. И конечно, мы можем только восхищаться, при этом никогда не сможем повторить нечто даже приближенное на своем домашнем ПК. Но поверьте: «не так страшен черт, как его малюют». Давайте попробуем разобраться, что же представляют из себя нейронные сети, и как можно их применить в нашей торговле.
Принципы построения искусственных нейронных сетей
В Википедии дано такое определение нейросети:
«Иску́сственная нейро́нная се́ть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.»
Т.е. искусственная нейронная сеть — это некая сущность, состоящая из массива искусственных нейронов с организованной взаимосвязью между ними. При этом организация взаимосвязей между нейронами создана по образу и подобию процессов в мозгу живого организма.
На рисунке ниже представлена схема простой нейронной сети. На ней кружочками обозначены нейроны, а линиями показаны связи между нейронами. Как видно на рисунке, нейроны расположены слоями, которые делят на 3 группы. Синим цветом обозначен слой входных нейронов на которые подается исходная информация. Зеленым и красным обозначены выходные нейроны, которые выдают результат работы нейронной сети. Между ними расположены серые нейроны, образующие, так называемый скрытый слой.
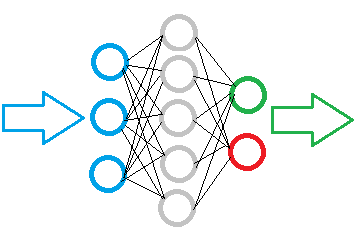

Несмотря на различие слоев, вся нейронная сеть построена из одинаковых нейронов, имеющих несколько элементов для входных сигналов и только один для выдачи результата. Внутри нейрона организована обработка поступившей информации с выдачей простого логического результата. К примеру, «Да» или «Нет». Применительно к теме торговли это может быть сигнал на сделку или указывать ее направление.
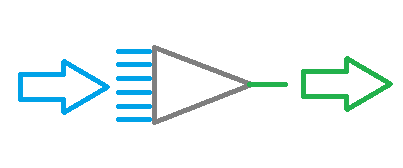

Исходная информация попадает на слой входных нейронов, обрабатывается и результат работы нейронов служит исходной информацией для нейронов последующего слоя. Операции повторяются от одного слоя к другому, пока не будет достигнут слой выходных нейронов. Таким образом, исходная информация обрабатывается и фильтруется от слоя к слою и на выходе нейронная сеть выдает некий результат.
В зависимости от сложности решаемых задач и создаваемых моделей количество нейронов в каждом слое может варьироваться. А также возможны вариации нейронных сетей с несколькими скрытыми слоями. Все это делает нейронную сеть более сложной, что позволяет решать более сложные задачи. Но в тоже время и требует больших вычислительных ресурсов.
Поэтому при создании своей модели нейронной сети нам нужно четко понимать какую информацию и в каком объеме мы будем обрабатывать, а также, что мы хотим получить в результате. От этого зависит количество необходимых нейронов в слоях модели.
Если мы хотим подать на вход нейронной сети некий массив данных из 10 элементов, то входной слой сети должен содержать 10 нейронов. Это позволит принять весь массив данных. Избыточные входные нейроны будут лишь балластом.
Количество выходных нейронов определяется ожидаемым результатом. Для получения однозначного логического результата достаточно одного выходного нейрона. Если требуется получить ответ на несколько вопросов, то необходимо создать по одному нейрону на каждый вопрос.
Скрытые слои нейронной сети являются неким аналитическим центром, который обрабатывает и анализирует полученную информацию. Следовательно, количество нейронов в слое зависит от вариативности данных предыдущего слоя, т.е. каждый нейрон предполагает некую гипотезу развития событий.
Количество скрытых слоев определяется причинно-следственной связью между исходными данными и ожидаемым результатом. К примеру, если мы строим нашу модель применительно к технике «5 почему», то логично использовать 4 скрытых слоя, которые в сумме с выходным слоем дадут возможность поставить 5 вопросов к исходным данным.
Подытожим:
- нейронная сеть строится из одинаковых нейронов, следовательно, для построения модели нам достаточно создать один класс нейронов;
- нейроны в модели организованы слоями;
- поток информации в нейронной сети организован в виде последовательной передачи данных через все слои модели от входных нейронов к выходным;
- количество входных нейронов обусловлено объемом анализируемой информации за один проход, а количество выходных нейронов — объемом результирующих данных;
- т.к. на выходе нейрона формируется некий логический результат, то и вопросы поставленные перед нейронной сетью должны предполагать однозначный ответ.
Как устроен искусственный нейрон
Получив представление о структуре нейронной сети, давайте рассмотрим построение модели искусственного нейрона. Ведь именно в его недрах осуществляются математические вычисления и принимается решения. И тут возникает вопрос: каким образом реализовать множество различных решений из одних исходных данных используя одну математическую формулу. Решение было найдено в изменении связей между нейронами. Для каждой связи определяется некий весовой коэффициент, который определяет влияние данного входного значения на результат принимаемого решения.
Математическая модель нейрона состоит из двух функций. Вначале суммируются произведения входных данных на их весовые коэффициенты.
А затем на основании полученного значения вычисляется результирующее значение в, так называемой, функции активации. На практике применяются различные варианты функции активации, но наибольшее распространение получили такие функции:
- Сигмовидная функция — диапазон возвращаемых значений от «0» до «1»
- Гиперболический тангенс — диапазон возвращаемых значений от «-1» до «1»
Выбор функции активации зависит от решаемых задач. Так, если в результате обработки исходных данных ожидаем получить логический ответ, то предпочтение отдается сигмовидной функции. В реалиях трейдинга, я предпочитаю использовать гиперболический тангенс. Где значение «-1» соответствует сигналу на продажу, а значение «1» — сигналу на покупку. Результат между пороговыми значениями говорит о некой неопределенности.
Обучение сети
Как выше было сказано, вариативность результатов каждого нейрона и нейронной сети в целом зависит от подобранных весовых коэффициентов для связей между нейронами. Решение задачи подбора правильных весовых коэффициентов называется обучением нейронной сети.
Для обучения нейронной сети существуют различные алгоритмы и методы:
- Обучение с учителем;
- Обучение без учителя;
- Обучение с подкреплением.
Метод обучения определяется от наличия исходных данных и поставленных перед нейронной сетью задач.
Обучение с учителем используется при наличии достаточного набора исходных данных с соответствующими правильными ответами на поставленные вопросы. В процессе обучения на вход нейронной сети подаются исходные данные и полученный на выходе сети результат сверяется с заведомо известным правильным ответом. После чего корректируются веса в сторону снижения ошибки.
Обучение без учителя применяется при наличии массива исходных данных и отсутствии правильных ответов на поставленные вопросы. При таком обучении нейронная сеть ищет схожие наборы данных и позволяет разделить исходные данные на схожие группы.
Обучение с подкреплением применяется когда нет правильных ответов, но есть понимание того, что должны получить в итоге. В ходе обучения на вход нейросети подаются исходные данные и сеть пытается решить задачу. После проверки результата дается обратная связь сети в виде определенной награды. В процессе обучения нейронная сеть стремиться к максимальной награде.
В данной статье мы будем использовать обучение с учителем. В качестве примера я выбрал метод обратного распространения ошибки. Такой подход позволяет организовать постоянное обучение нейронной сети в режиме реального времени.
В основе данного метода лежит использование выходной ошибки нейронной сети для коррекции ее весов. Сам алгоритм обучения состоит из двух этапов. Вначале на основании входных данных рассчитывается результирующее значение нейронной сети, которое сравнивается с эталонным и вычисляется ошибка. Далее осуществляется обратный проход с распространением ошибки от выхода сети к ее входам с коррекцией всех весовых коэффициентов. Данный подход итеративный и обучение сети осуществляется пошагово, что позволяет после обучения на исторических данных перейти к обучению сети в режиме online.
Метод обратного распространения ошибки использует стохастический градиентный спуск, что позволяет достичь приемлемого минимума ошибки. А благодаря возможности обучения нейронной сети online, поддерживать этот минимум на длительном временном интервале.
Строим свою нейронную сеть средствами MQL
После осмысления теории работы нейронных сетей можно перейти к практической части статьи. Чтобы лучше показать алгоритм работы НС, я предлагаю сделать пример полностью средствами языка MQL5 без использования сторонних библиотек. И начнем мы работу с создания классов для хранения данных об элементарных связях между нейронами.
4.1. Связи
Вначале создадим класс СConnection для хранения весового коэффициента одной связи. И создадим его наследником класса CObject. Данный класс будет содержать две переменные типа double: weight для хранения непосредственно значения весового коэффициента и deltaWeight, в которой будем хранить величину последнего изменения весового коэффициента (используется при обучении). Чтобы не использовать дополнительные методы для работы с переменными сделаем их публичными. Начальное значение переменных будет задаваться в конструкторе класса.
class СConnection : public CObject { public: double weight; double deltaWeight; СConnection(double w) { weight=w; deltaWeight=0; } ~СConnection(){}; //— methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); };
Также, для возможности последующего сохранения информации о связях создадим методы сохранения данных в файл Save и последующего чтения Load. Данные методы построены по классической схеме с получением хендла файла в параметрах метода, проверяем его состоятельность и записываем данные (или считываем в методе Load).
bool СConnection::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; //— if(FileWriteDouble(file_handle,weight)<=0) return false; if(FileWriteDouble(file_handle,deltaWeight)<=0) return false; //— return true; }
Следующим шагом создадим массив для хранения весов CArrayCon на базе класса CArrayObj. Здесь мы переопределим два виртуальных метода CreateElement и Type. Первый будет использоваться для создания нового элемента, а второй будет идентифицировать наш класс.
class CArrayCon : public CArrayObj { public: CArrayCon(void){}; ~CArrayCon(void){}; //— virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7781); } };
В параметрах метода создания нового элемента CreateElement будем передавать индекс создаваемого элемента. В самом методе проверим его действительность, проверим размер массива хранения данных и изменим его при необходимости. А затем создадим новый экземпляр класса СConnection, задав начальный вес случайной величиной.
bool CArrayCon::CreateElement(const int index) { if(index<0) return false; //— if(m_data_max1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //— m_data[index]=new СConnection(MathRand()/32767.0); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; m_data_total=MathMax(m_data_total,index); //— return (true); }
4.2. Нейрон
Следующим шагом создадим искусственный нейрон. Как я уже писал выше, в качестве функции активации для своего нейрона я использую гиперболический тангенс. Диапазон результирующих значений данной функции лежит от «-1» до «1». Значение «-1» дает сигнал на продажу, а «1» — на покупку.
Класс искусственного нейрона CNeuron, также как и предыдущий элемент СConnection, создадим наследником класса CObject, но его структура будет немного сложнее.
class CNeuron : public CObject { public: CNeuron(uint numOutputs,uint myIndex); ~CNeuron() {}; void setOutputVal(double val) { outputVal=val; } double getOutputVal() const { return outputVal; } void feedForward(const CArrayObj *&prevLayer); void calcOutputGradients(double targetVals); void calcHiddenGradients(const CArrayObj *&nextLayer); void updateInputWeights(CArrayObj *&prevLayer); //— methods for working with files virtual bool Save(const int file_handle) { return(outputWeights.Save(file_handle)); } virtual bool Load(const int file_handle) { return(outputWeights.Load(file_handle)); } private: double eta; double alpha; static double activationFunction(double x); static double activationFunctionDerivative(double x); double sumDOW(const CArrayObj *&nextLayer) const; double outputVal; CArrayCon outputWeights; uint m_myIndex; double gradient; };
В параметрах конструктора класса передадим количество исходящих связей нейрона и его порядковый номер в слое (потребуется для последующей идентификации нейрона). В теле метода зададим константы, сохраним полученные данные и создадим массив исходящих связей.
CNeuron::CNeuron(uint numOutputs, uint myIndex) : eta(0.15), // net learning rate alpha(0.5) // momentum { for(uint c=0; c
Методы setOutputVal и getOutputVal служат для обращения к результирующему значению нейрона. Непосредственный расчет результирующего значения нейрона осуществляется в методе feedForward. В параметрах данный метод получает предшествующий слой нейронов.
void CNeuron::feedForward(const CArrayObj *&prevLayer) { double sum=0.0; int total=prevLayer.Total(); for(int n=0; nIsStopped(); n++) { CNeuron *temp=prevLayer.At(n); double val=temp.getOutputVal(); if(val!=0) { СConnection *con=temp.outputWeights.At(m_myIndex); sum+=val * con.weight; } } outputVal=activationFunction(sum); }
В теле метода организован цикл по перебору всех нейронов предыдущего слоя и суммирования произведения результирующих значений нейронов с весовыми коэффициентами. После расчета суммы вычисляется результирующее значение нейрона в методе activationFunction (функция активации нейрона вынесена в отдельный метод).
double CNeuron::activationFunction(double x) { //output range [-1.0..1.0] return tanh(x); }
Следующий блок методов используется при обучении нейронной сети. Вначале создадим метод вычисления производной для функции активации activationFunctionDerivative. Это необходимо чтобы определить какое требуется изменение суммирующей функции для компенсации ошибки результирующего значения нейрона.
double CNeuron::activationFunctionDerivative(double x) { return 1/MathPow(cosh(x),2); }
Далее создаем два метода расчета градиента для корректировки весовых коэффициентов. Необходимость создания 2-х методов обусловлена различием в расчете ошибки результирующего значения для нейронов выходного слоя и скрытых слоев. Для выходного слоя ошибка рассчитывается как разница результирующего и эталонного значения, в то время как для нейронов скрытых слоев ошибка рассчитывается как сумма градиентов всех нейронов последующего слоя взвешенных на весовые коэффициенты связей между нейронами. Данный расчет вынесен в отдельный метод sumDOW.
void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer) { double dow=sumDOW(nextLayer); gradient=dow*CNeuron::activationFunctionDerivative(outputVal); } //+——————————————————————+ //| | //+——————————————————————+ void CNeuron::calcOutputGradients(double targetVals) { double delta=targetVals-outputVal; gradient=delta*CNeuron::activationFunctionDerivative(outputVal); }
Затем градиент определяется как произведение ошибки на производную от функции активации.
Рассмотрим детальнее метод определения ошибки нейрона скрытого слоя sumDOW. В параметрах данные метод получает указатель на последующий слой нейронов. В теле метода сначала обнуляем итоговую переменную sum, затем организуем цикл по перебору всех нейронов последующего слоя и просуммируем произведение градиентов нейронов на весовой коэффициент связи с ним.
double CNeuron::sumDOW(const CArrayObj *&nextLayer) const { double sum=0.0; int total=nextLayer.Total()-1; for(int n=0; nreturn sum; }
После проведенной выше подготовительной работы осталось создать метод пересчета весовых коэффициентов updateInputWeights. В моей модели нейрон хранит исходящие весовые коэффициенты, поэтому метод обновления весовых коэффициентов получает в параметрах предшествующий слой нейронов.
void CNeuron::updateInputWeights(CArrayObj *&prevLayer) { int total=prevLayer.Total(); for(int n=0; nIsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); СConnection *con=neuron.outputWeights.At(m_myIndex); con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight; } }
В теле метода создан цикл по перебору всех нейронов предыдущего слоя с корректировкой их весовых коэффициентов влияния именно на текущий нейрон.
Хочу обратить внимание, что корректировка весов осуществляется с применением двух коэффициентов eta (притупляет реакцию на текущее отклонение) и alpha (коэффициент инертности). Подобный подход помогает в некоторой мере усреднить влияние ряда последующих итераций обучения и отсеять шумовые данные.
4.3. Нейронная сеть
После создания искусственного нейрона нам предстоит объединить созданные объекты в единую сущность — нейронную сеть. Мы должны понимать, что создаваемые объекты должны быть гибкими и позволять создавать нейронные сети различных конфигураций. Это позволит нам воспользоваться плодами наших трудов для решения различных задач.
Как уже писалось выше, нейронная сеть состоит из слоев нейронов. Следовательно, первое, что мы сделаем, это объединим нейроны в слой. Для этого создадим класс CLayer, унаследовав основные методы от класса CArrayObj.
class CLayer: public CArrayObj { private: uint iOutputs; public: CLayer(const int outputs=0) { iOutputs=outpus; }; ~CLayer(void){}; //— virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7779); } };
В параметрах метода инициализации класса CLayer зададим количество элементов последующего слоя. А также мы перепишем два виртуальных метода CreateElement (создание нового нейрона слоя) и Type (метод идентификации объекта).
При создании нового нейрона укажем его порядковый номер в параметрах метода. В теле метода сначала проверим действительность полученного индекса. Затем проверим размер массива для хранения указателей на экземпляры объектов нейрона, при необходимости увеличим размер массива. Далее создадим новый нейрон. При успешном создании нового экземпляра нейрона, зададим его начальное значение и изменим количество объектов в массиве и выходим из метода с результатом true.
bool CLayer::CreateElement(const uint index) { if(index<0) return false; //— if(m_data_max1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //— CNeuron *neuron=new CNeuron(iOutputs,index); if(!CheckPointer(neuron)!=POINTER_INVALID) return false; neuron.setOutputVal((neuronNum%3)-1) //— m_data[index]=neuron; m_data_total=MathMax(m_data_total,index); //— return (true); }
Аналогичным подходом создадим класс CArrayLayer для хранения указателей на слои нашей сети.
class CArrayLayer : public CArrayObj { public: CArrayLayer(void){}; ~CArrayLayer(void){}; //— virtual bool CreateElement(const uint neurons, const uint outputs); virtual int Type(void) const { return(0x7780); } };
Отличие от предыдущего класса можно увидеть в специфике метода создания нового элемента массива CreateElement. В параметры этого метода передадим количество нейронов в создаваемом и последующем слоях. В теле метода поверим количество нейронов в создаваемом слое. При отсутствии нейронов в создаваемом слое, выходим из метода с значением false. Далее проверяем необходимость изменения размера массива для хранения указателей. И затем переходим непосредственно к созданию экземпляров объектов: создаем новый слой и организовываем цикл по созданию нейронов. На каждом шаге проверяем созданный объект. При появлении ошибки выходим из метода с значением false. После создания всех элементов сохраняем в массиве указатель на созданный слой и выходим из метода с результатом true.
bool CArrayLayer::CreateElement(const uint neurons, const uint outputs) { if(neurons<=0) return false; //— if(m_data_max<=m_data_total) { if(ArrayResize(m_data,m_data_total+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //— CLayer *layer=new CLayer(outputs); if(!CheckPointer(layer)!=POINTER_INVALID) return false; for(uint i=0; iif(!layer.CreatElement(i)) return false; //— m_data[m_data_total]=layer; m_data_total++; //— return (true); }
Создание отдельных классов для слоя и массива слоев позволяет нам создавать нейронные сети различной конфигурации без изменения самих классов. Мы получили довольно гибкую сущность, позволяющая извне задавать количество слоев и нейронов в каждом слое.
И наконец переходим к созданию класса нашей нейронной сети CNet.
class CNet { public: CNet(const CArrayInt *topology); ~CNet(){}; void feedForward(const CArrayDouble *inputVals); void backProp(const CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals); double getRecentAverageError() const { return recentAverageError; } bool Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //— static double recentAverageSmoothingFactor; private: CArrayLayer layers; double recentAverageError; };
Благодаря проделанной выше работе сам класс нейронной сети содержит минимум переменных и методов. В представленном коде только две статические переменные для расчета и хранения средней ошибки (recentAverageSmoothingFactor и recentAverageError) и указатель на массив слоев нашей нейронной сети layers.
Давайте подробнее остановимся на методах данного класса. В параметрах конструктора класса передается указатель на массив данных типа int. Количество элементов в массиве указывает на количество слоев в создаваемой нейронной сети, а каждый элемент массива содержит количество нейронов в соответствующем слое. Таким образом, мы делаем наш класс универсальным для создания практически любой сложности нейронной сети.
CNet::CNet(const CArrayInt *topology) { if(CheckPointer(topology)==POINTER_INVALID) return; //— int numLayers=topology.Total(); for(int layerNum=0; layerNumuint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1)); if(!layers.CreateElement(topology.At(layerNum), numOutputs)) return; } }
В теле метода проверяем действительность переданного указателя и организовываем цикл по созданию слоев нейронной сети. Надо сказать, что для выходного слоя нейронов указывается нулевое количество выходных связей.
Метод feedForward предназначен для расчета значения нейронной сети. В параметрах метод получает массив входных значений, на основании которых будут рассчитываться результирующие значения нейронной сети.
void CNet::feedForward(const CArrayDouble *inputVals) { if(CheckPointer(inputVals)==POINTER_INVALID) return; //— CLayer *Layer=layers.At(0); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=inputVals.Total(); if(total!=Layer.Total()-1) return; //— for(int i=0; iIsStopped(); i++) { CNeuron *neuron=Layer.At(i); neuron.setOutputVal(inputVals.At(i)); } //— total=layers.Total(); for(int layerNum=1; layerNumIsStopped(); layerNum++) { CArrayObj *prevLayer = layers.At(layerNum — 1); CArrayObj *currLayer = layers.At(layerNum); int t=currLayer.Total()-1; for(int n=0; nIsStopped(); n++) { CNeuron *neuron=currLayer.At(n); neuron.feedForward(prevLayer); } } }
В теле метода проверим действительность полученного указателя и нулевого слоя нашей сети. Затем полученные исходные данные зададим в качестве результирующих значений нейронов нулевого слоя и организуем двойной цикл с поэтапным пересчетом результирующих значений нейронов по всей нейронной сети от первого скрытого слоя до выходных нейронов.
Для получения самого результата предназначен метод getResults, в котором организован цикл по сбору результирующих значений с нейронов выходного слоя.
void CNet::getResults(CArrayDouble *&resultVals) { if(CheckPointer(resultVals)==POINTER_INVALID) { resultVals=new CArrayDouble(); } resultVals.Clear(); CArrayObj *Layer=layers.At(layers.Total()-1); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=Layer.Total()-1; for(int n=0; n
Процесс обучения нейронной сети построен в методе backProp. В параметрах метод получает массив эталонных значений. В теле метода проверяем действительность полученного массива и считаем среднеквадратичную ошибку результирующего слоя. Затем в цикле пересчитываем градиенты нейронов во всех слоях. После чего в последнем цикле метода актуализируем весовые коэффициенты связей между нейронами на основании рассчитанных ранее градиентов.
void CNet::backProp(const CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return; CArrayObj *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //— double error=0.0; int total=outputLayer.Total()-1; for(int n=0; nIsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double delta=targetVals[n]-neuron.getOutputVal(); error+=delta*delta; } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor; //— for(int n=0; nIsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); neuron.calcOutputGradients(targetVals.At(n)); } //— for(int layerNum=layers.Total()-2; layerNum>0; layerNum—) { CArrayObj *hiddenLayer=layers.At(layerNum); CArrayObj *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; nIsStopped();++n) { CNeuron *neuron=hiddenLayer.At(n); neuron.calcHiddenGradients(nextLayer); } } //— for(int layerNum=layers.Total()-1; layerNum>0; layerNum—) { CArrayObj *layer=layers.At(layerNum); CArrayObj *prevLayer=layers.At(layerNum-1); total=layer.Total()-1; for(int n=0; nIsStopped(); n++) { CNeuron *neuron=layer.At(n); neuron.updateInputWeights(prevLayer); } } }
Чтобы не переобучать нашу нейронную сеть при перезапуске программы, создадим методы сохранения данных в локальный файл Save и последующей загрузки данных из файла Load.
Более подробно с кодом всех методов класса можно ознакомиться во вложении.
Заключение
В данной статье я попытался рассказать и показать как можно создать нейронную сеть для своих нужд в домашних условиях. Конечно, это лишь вершина айсберга. И в статье рассмотрен лишь один из возможных вариантов — перцептрон, предложенный Фрэнком Розенблаттом в далеком 1957 году. С тех пор прошло уже более 60 лет и появились другие модели. Но данная модель по прежнему жизнеспособна и дает неплохие результаты, в чем каждый может удостовериться на собственном опыте. Для желающих более глубоко погрузиться в тему искусственного интеллекта я посоветую обратиться к соответствующей литературе, т.к. полностью раскрыть труды ученых мужей не возможно даже в серии статей.
Ссылки
- Википедия
- Перцептрон
Программы, используемые в статье:
| # | Имя | Тип | Описание |
| 1 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети (перцетрона) |
Нейроны как логические элементы
К анализу поведения нейронов можно подойти с позиций математической логики. Для этого сконцентрируемся на одном классе задачи xor, например на крестиках. Запишем логическое условие которому удовлетворяют все объекты этого класса. В примере выше: «любой крестик лежит по вектору плоскости A
и по вектору плоскости
B
«. Это кратко можно выразить формулой
A & B
. Выходной нейрон «
C
» реализует такое логическое «И». Действительно, его плоскость прижата к правому нижнему углу квадрата в пространстве признаков с координатами
(1,1)
. Поэтому для входов (поставляемых нейронами «
A
» и «
B
«) близких к единице, на выходе этого нейрона будет
1
(точнее его значение больше
0.5
). Поэтому, как и положено,
1 & 1 = 1
. Если хотя бы один из входов отличен от
1
, то и выход будет нулевым (меньшим
0.5
). Это справедливо и в пространстве произвольной размерности, где гиперплоскость нейрона, обеспечивающего логическое «И» прижата к углу гиперкуба с координатами
(1,1,…,1)
(отсекает его от остального гиперкуба).
Если плоскость сместить в угол (0,0)
, сохранив направление нормали к углу
(1,1)
, то такой нейрон будет логическим «ИЛИ». Его функция
y=S(x1,x2)
даёт
S(0,0)=0
и в остальных случаях
1
(ниже первый рисунок):
В общем случае, плоскость нейрона, реализующего логическое «ИЛИ» отсекает угол (0,0,…,0)
n
-мерного куба, а вектор его нормали направлен в сторону большего объём гиперкуба. В отличии от этого, стандартное логическое «И» (второй рисунок) имеет вектор нормали в сторону меньшего объёма.
Логическое «И» для нейрона с n
входами описывается следующей функцией:
y = S( w·(x1+…+xn+α-n) )
,
y = x1 & x2 & … & xn
,
где параметр α — параметр, лежащий в диапазоне 0<�α<1
. Чем он ближе к нулю, тем сильнее плоскость прижата к углу с координатами
(1,1,…,1)
. Действительно, когда
α=0
и
x1=…=xn=1
, имеем
x1+…+xn-n=0
. Чтобы этот нейрон обеспечивал логическое И, он должен давать отрицательное расстояние к «ближайшему» углу гиперкуба у которого одна координата равна нулю:
(1,…,1,0,1,…,1)
. Это даёт ограничение
α<1
. Общий множитель
w
характеризует длину нормали (чем он больше, тем более уверен в себе нейрон). Сигмоидная функция
S(d)
приведена в начале документа.
Аналогично записывается функция логического «ИЛИ» (0<�α<1
)
y = S( w·(x1+…+xn-α) )
,
y = x1 ∨ x2 ∨ … ∨ xn
.
Ещё одна логическая функция отрицания реализуется при помощи вычитания. Обозначим её чертой над именем переменной. Тогда x
=
1-x
и, как обычно,
0=1
,
1=0
. Если один из входов нейронов имеет отрицание, то его функция выхода имеет вид:
y = S( w·(-x1+…+xn+α-n+1) )
,
y = x1 & x2 & … & xn
.
Таким образом, одна из компонент вектора нормали меняет свой знак и плоскость нейрона сдвигается. Выше на третьем и четвёртом рисунках приведены различные отрицания перменных. Стоит в этих терминах получить логическое ИЛИ из логического И при помощи правила де-Моргана:
!(x1 & x2) = x1 ∨ x2
,
где восклицательный знак — ещё один способ обозначения логического отрицания.
Теперь посмотрим, как это работает на практике
Пусть у нас имеется однослойный перцептрон с одним выходом и линейной активационной функцией . Её производная равна 1 для всех . Пусть количество входов , веса инициализированы нулями и есть обучающая выборка из одного элемента: .
Промоделируем, как будет осуществляться обучение с коэффициентом скорости обучения .
Вспомним формулы
| Шаг | Начальное значение | |||
| 1 | (0; 0; 0) | 0 | -42 | (4,2; 16,8; 8,4) |
| 2 | (4,2; 16,8; 8,4) | 44,1 | 2,1 | (-0,21; -0,84; -0,42) |
| 3 | (3,99; 15,96; 7,98) | 41,895 | -0,105 | (0,0105; 0,042; 0,021) |
| 4 | (4,005; 16,002; 8,001) | 42,00525 | 0,00525 | (-0,00053; -0,0021; -0,00105) |
| 5 | (3,99998; 15,9999; 7,99995) | 41,99974 | -0,00026 | (0,00003; 0,00010; 0,00005) |
| 6 | (4,00000; 16,00001; 8,00000) | 42,00001 | 0,00001 |
Здесь все числа приведены с точностью до 5 знаков после запятой.
Как видно, перцептрон довольно быстро пришёл к значениям весов, близких к . При значение выхода равно , а величина ошибки равна нулю.
То есть перцептрон вполне успешно обучился, стартуя с весов, инициализированных нулями. Причём, что важно, все веса получились различными.
Аппроксимация функции y=f(x)
При помощи нейронной сети с одним входом, одним выходом и достаточно большим скрытым слоем, можно аппроксимировать любую функцию y=f(x)
. Для доказательства, создадим сначала сеть, которая на выходе даёт
1
, если вход лежит в диапазоне
[a…b]
и
0
— в противном случае.
Пусть σ(d) = S(ω·d)
— сигмоидная функция, аргумент которой умножен на большое число
ω
, так что получается прямоугольная ступенька. При помощи двух таких ступенек, можно создать столбик единичной высоты:
Нормируем аппроксимируемую функцию y=f(x)
на интервал
[0…1]
как для её аргумента
x
, так и для значения
y
. Разобъём диапазон изменения
x=[0…1]
на большое число интервалов (не обязательно равных). На каждом интервале функция должна меняется незначительно. Ниже приведено два таких интервала:
Каждая пара нейронов в скрытом слое реализует единичный столбик. Величина d
равна
w1
, если
x∈(a,b)
и
w2
, если
x∈(b,с)
. Если выходной нейрон является линейным сумматором, то можно положить
wi=fi
, где
fi
— значения функции на каждом интервале. Если же выходной нейрон — обычный нелинейный элемент, то необходимо пересчитать веса
wi
при помощи обратной к сигмоиду функции (последняя формула).
Losses
Функции потерь — это очень важная вещь, которую следует учитывать при создании нейронной сети, потому что функции потерь в нейронной сети будут вычислять разницу между прогнозируемым выходом и фактическим результатом и очень помогают оптимизаторам в нейронных сетях обновлять веса при его обратном распространении.
Есть много функций потерь, которые поддерживаются библиотекой TensorFlow, и, опять же, обычно используются лишь некоторые из них:
- Mean Absolute
- MeanSquaredError
- Binary Crossentropy
- Categorical Crossentropy
- Sparse Categorica Crossentropy
Примечание. Опять же, выбор потерь полностью зависит от типа проблемы и результата, который мы ожидаем от нейронной сети.
Аппроксимация функции на Phyton
Ниже приведен код на языке Phyton, который аппроксимирует функцию y=sin(pi*x)
:
import numpy as np # библиотека численных методов import matplotlib.pyplot as plt # библиотека рисования графиков def F(x): # эту функцию аппроксимируем return np.sin(np.pi*x); n=10 # число интервалов x1 = np.arange(0, 1, 1/n) # координаты левых границ x2 = np.arange(1/n, 1+1/n, 1/n) # координаты правых границ print(«x1:»,x1,»\nx2:»,x2) # выводим эти массивы f = F( (x1+x2)/2 ) # функция в середине интервала fi = np.log( f/(1-f) ) # обратные значения к сигмоиду def S(z, z0, s): # сигмоид return 1/(1+np.exp(-100*s*(z-z0))) def Net(z): # выход сети return 1/(1+np.exp(-np.dot(fi, S(z, x1, 1) + S(z, x2, -1) -1))) x = np.arange(0.01, 1, 0.01) # массив x-ов y = [ Net(z) for z in x ] # массив y-ов (выход сети) plt.plot(x, y) # результаты работы plt.plot(x, F(x)) # исходная функция plt.show() # показываем картинку
В результате работы, при n=10
и
n=100
получаются следующие результаты: