Эта статья представляет собой вводный материал по машинному обучению (Machine Learning). Вы узнаете про основные задачи, виды и функции обучения на моделях, ознакомитесь с некоторыми алгоритмами (algorithms) и особенностями моделирования (modelling). Статья сможет дать ответы и на многие другие вопросы.
Сегодня ML (Machine Learning) решает множество задач, упрощая многим жизнь. Достаточно заложить в ПК алгоритм (algorithm) нахождения решений, чтобы получить возможность комплексно использовать статистические данные и выводить различные закономерности, делать прогнозы.
Технология machines-обучения появилась в середине прошлого века, когда стали появляться первые программы игры в шашки. С годами суть мало изменилась. Но изменились вычислительные мощности наших компьютеров, в результате усложнились закономерности и прогнозы, увеличилось число задач и решаемых проблем.
Чтобы процесс обучения был запущен, нужно загрузить исходные данные, называемые датасетом. Если хотите, пусть это будут изображения животных с метками. Именно на них алгоритм станет обучаться обработке запросов. Когда обучение закончится, модель сможет самостоятельно распознавать нужные изображения, а метки больше не понадобятся. Но обучение на этом не прекратится совсем, а будет продолжаться и дальше по мере использования программы. Чем больше данных будет в итоге проанализировано, тем точнее будет распознавание.
Сегодня ML распознаёт и рисунки, и лица, и пейзажи, и числа, и буквы, и предметы. Та же функция машинного обучения по проверке грамматики есть почти в каждом текстовом редакторе. И учитывает эта функция как орфографию, так и другие моменты, включая лексические сочетания, жаргонизмы и прочие тонкости «великого и могучего». Есть и программы, которые сами генерируют новостные тексты — даже участие человека не требуется (копирайтеры, задумайтесь!)
Основные термины
В системах машинного обучения или же системах нейросетей существуют входы и выходы. То, что подаётся на входы, принято называть признаками (англ. features).
Lead Software Engineer, Infrastructure
Cube Dev, Удалённо, От 8000 $
tproger.ru
Вакансии на tproger.ru
Признаки по существу являются тем же, что и переменные в научном эксперименте — они характеризуют какой-либо наблюдаемый феномен и их можно как-то количественно измерить.
Когда признаки подаются на входы системы машинного обучения, эта система пытается найти совпадения, заметить закономерность между признаками. На выходе генерируется результат этой работы.
Этот результат принято называть меткой (англ. label), поскольку у выходов есть некая пометка, выданная им системой, т. е. предположение (прогноз) о том, в какую категорию попадает выход после классификации.
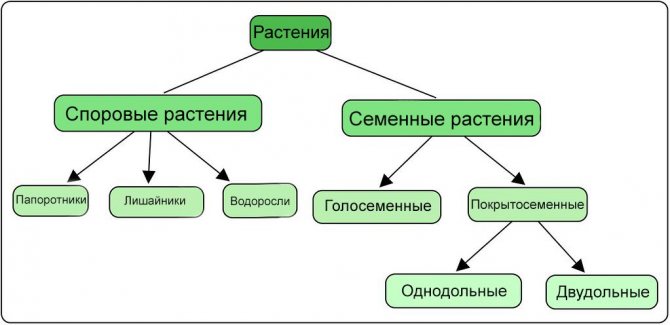
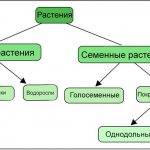
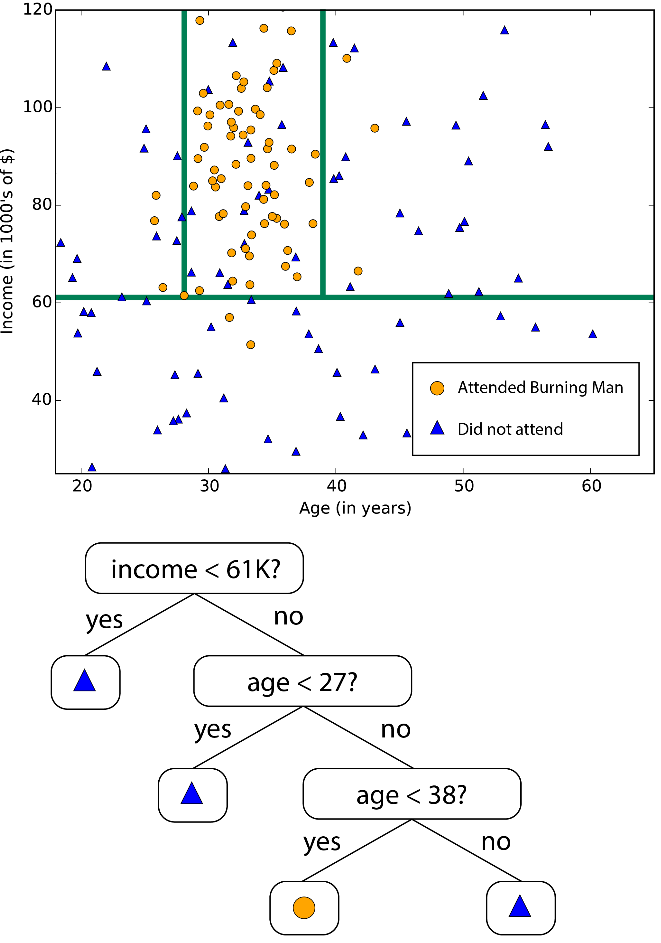
В контексте машинного обучения классификация относится к обучению с учителем. Такой тип обучения подразумевает, что данные, подаваемые на входы системы, уже помечены, а важная часть признаков уже разделена на отдельные категории или классы. Поэтому сеть уже знает, какая часть входов важна, а какую часть можно самостоятельно проверить. Пример классификации — сортировка различных растений на группы, например «папоротники» и «покрытосеменные». Подобная задача может быть выполнена с помощью Дерева Решений — одного из типов классификатора в Scikit-Learn.
При обучении без учителя в систему подаются непомеченные данные, и она должна попытаться сама разделить эти данные на категории. Так как классификация относится к типу обучения с учителем, способ обучения без учителя в этой статье рассматриваться не будет.
Процесс обучения модели — это подача данных для нейросети, которая в результате должна вывести определённые шаблоны для данных. В процессе обучения модели с учителем на вход подаются признаки и метки, а при прогнозировании на вход классификатора подаются только признаки.
Принимаемые сетью данные делятся на две группы: набор данных для обучения и набор для тестирования. Не стоит проверять сеть на том же наборе данных, на которых она обучалась, т. к. модель уже будет «заточена» под этот набор.
Выбор модели, переобучение
Может показаться, что мы вас обманули, когда пугали сложностями: очевидно, что для любой задачи машинного обучения можно построить идеальную модель, надо всего лишь запомнить всю обучающую выборку с ответами. Такая модель может достичь идеального качества по любой метрике, но радости от неё довольно мало, ведь мы хотим, чтобы она выявила какие-то закономерности в данных и помогла нам с ответами там, где мы их не знаем. Важно понимать, какая у построенной модели обобщающая способность, то есть насколько она способна выучить общие закономерности, присущие не только обучающей выборке, и давать адекватные предсказания на новых данных. Для того чтобы предохранить себя от конфуза, поступают обычно так: делят выборку с данными на две части: обучающую выборку и тестовую выборку (train и test). Обучающую выборку используют для собственно обучения модели, а метрики считают на тестовой.
Такой подход позволяет отделить модели, которые просто удачно подстроились к обучающим данным, от моделей, в которых произошла генерализация (generalization), то есть от таких, которые на самом деле кое-что поняли о том, как устроены данные, и могут выдавать полезные предсказания для объектов, которые не видели.
Например, рассмотрим три модели регрессионной зависимости, построенные на одном и том же синтетическом датасете с одним-единственным признаком. Жёлтым нарисованы точки обучающей выборки. Здесь мы представим, что есть «истинная» закономерность (пунктир), которая искажена шумом (погрешности измерения, влияние других факторов и т.д.).
Левая, линейная модель недостаточно хороша: она сделала, что могла, но плохо приближает зависимость, особенно при при маленьких и при больших $x$. Правая «запомнила» всю обучающую выборку (и в самом деле, чтобы вычислить значение этой функции, нам надо знать координаты всех исходных точек) вместо того, чтобы моделировать исходную зависимость. Наконец, центральная, хоть и не проходит через точки обучающей выборки, довольно неплохо моделирует истинную зависимость.
Алгоритм, избыточно подстроившийся под данные, называют переобученным.
С увеличением сложности модели ошибка на обучающей выборке падает. Во многих задачах очень сложная модель будет работать примерно так же, как модель, «просто запомнившая всю обучающую выборку», но с генерализацией всё будет плохо: ведь выученные закономерности будут слишком специфическими, подогнанными под то, что происходит на обучающей выборке. Мы видим это на трёх графиках сверху: линейная функция очень проста, но и закономерность приближает лишь очень грубо; на правом же графике мы видим довольно хитрую функцию, которая точно подобрана под значения из обучающей выборки, но явно слишком эксцентрична, чтобы соответствовать какой-то природной зависимости. Оптимальная же генерализация достигается на модели не слишком сложной и не слишком простой.
В качестве иллюстрации для того же самого датасета рассмотрим модели вида
\[y\ =\ \text{ многочлен степени }D\]
Ясно, что с ростом $D$ сложность модели растёт, и она достигает всё лучшего качества на обучающей выборке. А что, если у нас есть ещё тестовая выборка? Каким будет качество на ней? Вот так могут выглядеть графики среднеквадратичного отклонения (MSE) для обучающей и тестовой выборок:
Мы видим здесь типичную для классических моделей картину: MSE на обучающей выборке падает (может быть, даже до нуля), а на тестовой сперва падает, а затем начинает снова расти.
Замечание. Для моделей глубинного обучения всё немного интереснее: в некоторых ситуациях есть грань, за которой метрика на тестовой выборке снова начинает падать. Но об этом в своё время. Пока давайте запомним, что слишком сложная модель — это вредно, а переобучение — боль.
Точный способ выбрать алгоритм оптимальной сложности по данной задаче нам пока неизвестен, хотя какую-то теоретическую базу имеющимся философским наблюдениям мы дадим в главе про теорию обучения; при этом есть хорошо продуманная методология сравнения разных моделей и выбора среди них оптимальной — об этом мы обязательно расскажем вам в следующих главах. А пока дадим самый простой и неизменно ценный совет: не забывайте считать метрики на тестовой выборке и никогда не смешивайте её с обучающей!
Вопрос на подумать. Обсуждая переобучение, мы упоминали про сложность модели, но не сказали, что это такое. Как бы вы её определили? Как описать / сравнить сложность моделей для двух приведённых ниже задач? Почему, кстати, мы решили, что средняя модель ОК, а правая переобученная?
Ответ (не открывайте сразу; сначала подумайте сами!)
Сложность модели можно очень грубо охарактеризовать числом настраиваемых параметров модели, то есть тех, которые мы можем определить по данным в процессе обучения. Это не имеет никакого математического смысла, и о каких-то более серьёзных оценках мы поговорим в главе про теорию машинного обучения, но никто не бросит в вас камень, если вы скажете, что модель с 10 тысячами параметров сложнее, чем модель с 1000 параметров.
В первой задаче левая модель — это, судя по всему, линейная функция, у неё два параметра, вторая — наверное, квадратичная с тремя параметрами, а правая — многочлен какой-то высокой степени (на самом деле 11-й), у неё параметров намного больше. Центральная модель явно лучше, чем левая, справляется с тем, чтобы приблизить истинную закономерность; правая тоже вроде неплохо справляется с тем, чтобы приблизить её для обучающих данных, но вот два резких провала и крутое пике слева никак не объясняются имеющимися данными, и на двух тестовых точках в районе $0,5$ модель отчаянно врёт — так что есть причины считать, что она переобучилась.
Со второй задачей ситуация во многом похожая. Центральная модель явно лучше разделяет жёлтые и серые точки. На правой же картинке мы видим довольно неестественные выпячивания жёлтой и серой областей: например, к серой точке в центре картинки (которая наверняка была выбросом) протянулось серое «щупальце», захватившее и несколько тестовых (и даже обучающих) точек другого класса. В целом можно поспорить о том, плох ли правый классификатор, но он явно рисует слишком сложные границы, чтобы можно было поверить, что они отражают что-то из реальной жизни.
Типы классификаторов
Scikit-Learn даёт доступ ко множеству различных алгоритмов классификации. Вот основные из них:
- Метод k-ближайших соседей (K-Nearest Neighbors);
- Метод опорных векторов (Support Vector Machines);
- Классификатор дерева решений (Decision Tree Classifier) / Случайный лес (Random Forests);
- Наивный байесовский метод (Naive Bayes);
- Линейный дискриминантный анализ (Linear Discriminant Analysis);
- Логистическая регрессия (Logistic Regression);
На сайте Scikit-Learn есть много литературы на тему этих алгоритмов с кратким пояснением работы каждого из них.


Обзор самых популярных алгоритмов машинного обучения
tproger.ru
Метод k-ближайших соседей (K-Nearest Neighbors)
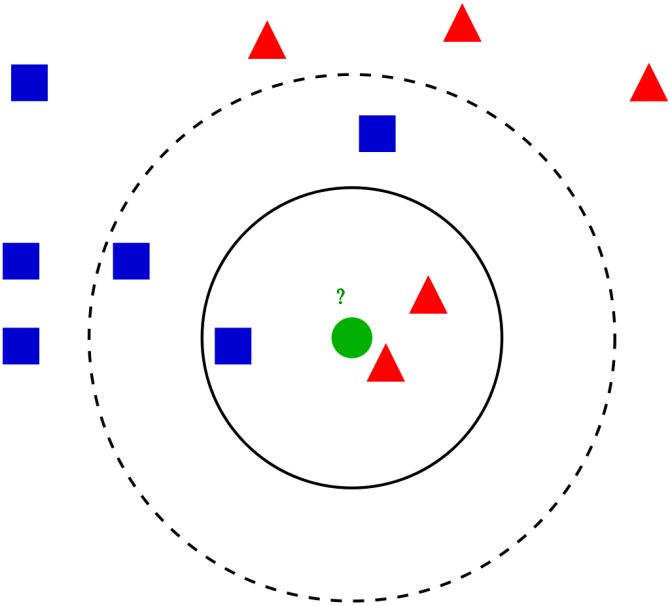

Этот метод работает с помощью поиска кратчайшей дистанции между тестируемым объектом и ближайшими к нему классифицированным объектами из обучающего набора. Классифицируемый объект будет относится к тому классу, к которому принадлежит ближайший объект набора.
Классификатор дерева решений (Decision Tree Classifier)
Этот классификатор разбивает данные на всё меньшие и меньшие подмножества на основе разных критериев, т. е. у каждого подмножества своя сортирующая категория. С каждым разделением количество объектов определённого критерия уменьшается.
Классификация подойдёт к концу, когда сеть дойдёт до подмножества только с одним объектом. Если объединить несколько подобных деревьев решений, то получится так называемый Случайный Лес (англ. Random Forest).
Наивный байесовский классификатор (Naive Bayes)
Такой классификатор вычисляет вероятность принадлежности объекта к какому-то классу. Эта вероятность вычисляется из шанса, что какое-то событие произойдёт, с опорой на уже на произошедшие события.
Каждый параметр классифицируемого объекта считается независимым от других параметров.
Линейный дискриминантный анализ (Linear Discriminant Analysis)
Этот метод работает путём уменьшения размерности набора данных, проецируя все точки данных на линию. Потом он комбинирует эти точки в классы, базируясь на их расстоянии от центральной точки.
Этот метод, как можно уже догадаться, относится к линейным алгоритмам классификации, т. е. он хорошо подходит для данных с линейной зависимостью.
Метод опорных векторов (Support Vector Machines)
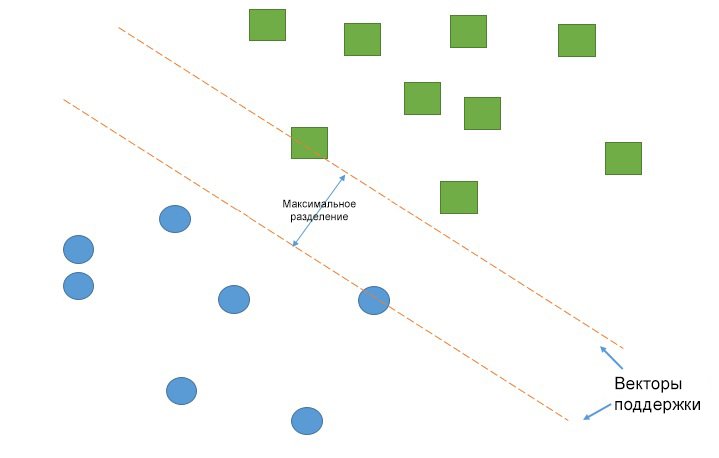

Работа метода опорных векторов заключается в рисовании линии между разными кластерами точек, которые нужно сгруппировать в классы. С одной стороны линии будут точки, принадлежащие одному классу, с другой стороны — к другому классу.
Классификатор будет пытаться увеличить расстояние между рисуемыми линиями и точками на разных сторонах, чтобы увеличить свою «уверенность» определения класса. Когда все точки построены, сторона, на которую они падают — это класс, которому эти точки принадлежат.
Логистическая регрессия (Logistic Regression)
Логистическая регрессия выводит прогнозы о точках в бинарном масштабе — нулевом или единичном. Если значение чего-либо равно либо больше 0.5, то объект классифицируется в большую сторону (к единице). Если значение меньше 0.5 — в меньшую (к нулю).
У каждого признака есть своя метка, равная только 0 или только 1. Логистическая регрессия является линейным классификатором и поэтому используется, когда в данных прослеживается какая-то линейная зависимость.
9 . Бэггинг и случайный лес
Случайный лес — очень популярный и эффективный алгоритм машинного обучения. Это разновидность ансамблевого алгоритма, называемого бэггингом.
Бутстрэп является эффективным статистическим методом для оценки какой-либо величины вроде среднего значения. Вы берёте множество подвыборок из ваших данных, считаете среднее значение для каждой, а затем усредняете результаты для получения лучшей оценки действительного среднего значения.
В бэггинге используется тот же подход, но для оценки всех статистических моделей чаще всего используются деревья решений. Тренировочные данные разбиваются на множество выборок, для каждой из которой создаётся модель. Когда нужно сделать предсказание, то его делает каждая модель, а затем предсказания усредняются, чтобы дать лучшую оценку выходному значению.
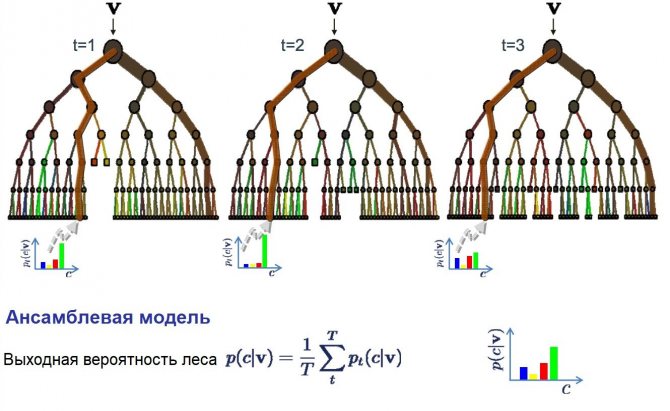

В алгоритме случайного леса для всех выборок из тренировочных данных строятся деревья решений. При построении деревьев для создания каждого узла выбираются случайные признаки. В отдельности полученные модели не очень точны, но при их объединении качество предсказания значительно улучшается.
Если алгоритм с высокой дисперсией, например, деревья решений, показывает хороший результат на ваших данных, то этот результат зачастую можно улучшить, применив бэггинг.
Примеры задач классификации
Задача классификации — эта любая задача, где нужно определить тип объекта из двух и более существующих классов. Такие задачи могут быть разными: определение, кошка на изображении или собака, или определение качества вина на основе его кислотности и содержания алкоголя.
В зависимости от задачи классификации вы будете использовать разные типы классификаторов. Например, если классификация содержит какую-то бинарную логику, то к ней лучше всего подойдёт логистическая регрессия.
По мере накопления опыта вам будет проще выбирать подходящий тип классификатора. Однако хорошей практикой является реализация нескольких подходящих классификаторов и выбор наиболее оптимального и производительного.
Линейный дискриминантный анализ (LDA)
Логистическая регрессия используется, когда нужно отнести образец к одному из двух классов. Если классов больше, чем два, то лучше использовать алгоритм LDA (Linear discriminant analysis).
Представление LDA довольно простое. Оно состоит из статистических свойств данных, рассчитанных для каждого класса. Для каждой входной переменной это включает:
- Среднее значение для каждого класса;
- Дисперсию, рассчитанную по всем классам.

Предсказания производятся путём вычисления дискриминантного значения для каждого класса и выбора класса с наибольшим значением. Предполагается, что данные имеют нормальное распределение, поэтому перед началом работы рекомендуется удалить из данных аномальные значения. Это простой и эффективный алгоритм для задач классификации.
Реализация классификатора
Первый шаг в реализации классификатора — его импорт в Python. Вот как это выглядит для логистической регрессии:
from sklearn.linear_model import LogisticRegression
Вот импорты остальных классификаторов, рассмотренных выше:
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.neighbors import KNeighborsClassifier from sklearn.naive_bayes import GaussianNB from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC
Однако, это не все классификаторы, которые есть в Scikit-Learn. Про остальные можно прочитать на соответствующей странице в документации.
После этого нужно создать экземпляр классификатора. Сделать это можно создав переменную и вызвав функцию, связанную с классификатором.
logreg_clf = LogisticRegression()
Теперь классификатор нужно обучить. Перед этим нужно «подогнать» его под тренировочные данные.
Обучающие признаки и метки помещаются в классификатор через функцию fit:
logreg_clf.fit(features, labels)
После обучения модели данные уже можно подавать в классификатор. Это можно сделать через функцию классификатора predict, передав ей параметр (признак) для прогнозирования:
logreg_clf.predict(test_features)
Эти этапы (создание экземпляра, обучение и классификация) являются основными при работе с классификаторами в Scikit-Learn. Но эта библиотека может управлять не только классификаторами, но и самими данными. Чтобы разобраться в том, как данные и классификатор работают вместе над задачей классификации, нужно разобраться в процессах машинного обучения в целом.
Линейная регрессия
Один из самых понятных и известных алгоритмов в машинном обучении и статистике. Его можно представить в форме уравнения, описывающего прямую, максимально точно показывающую взаимосвязь между выходными переменными y и входными переменными x. Чтобы составить уравнения, найдём определённые коэффициенты b для входных переменных.
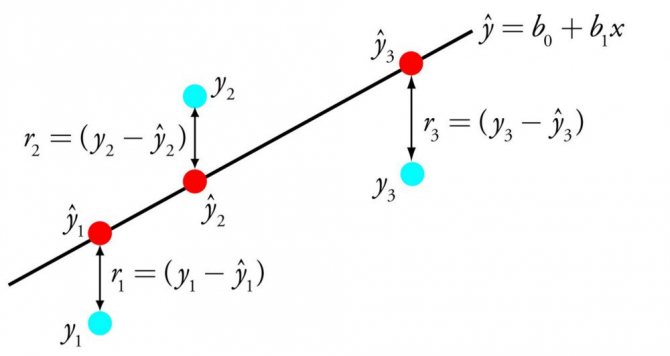

К примеру:
y = b0 + b1 * x
Зная x, мы должны найти y. Что касается цели этого алгоритма, то она состоит в поиске значений коэффициентов b0 и b1.
Чтобы оценить регрессионную модель, используют разные методы, например, метод наименьших квадратов. Вообще, линейная регрессия существует не одну сотню лет, поэтому алгоритм тщательно изучен. Он считается быстрым, простым и хорошо подходит для изучения в качестве первого алгоритма в машинном обучении.
Процесс машинного обучения
Процесс содержит в себе следующие этапы: подготовка данных, создание обучающих наборов, создание классификатора, обучение классификатора, составление прогнозов, оценка производительности классификатора и настройка параметров.
Во-первых, нужно подготовить набор данных для классификатора — преобразовать данные в корректную для классификации форму и обработать любые аномалии в этих данных. Отсутствие значений в данных либо любые другие отклонения — все их нужно обработать, иначе они могут негативно влиять на производительность классификатора. Этот этап называется предварительной обработкой данных (англ. data preprocessing).
Следующим шагом будет разделение данных на обучающие и тестовые наборы. Для этого в Scikit-Learn существует отличная функция traintestsplit.
Как уже было сказано выше, классификатор должен быть создан и обучен на тренировочном наборе данных. После этих шагов модель уже может делать прогнозы. Сравнивая показания классификатора с фактически известными данными, можно делать вывод о точности классификатора.
Вероятнее всего, вам нужно будет «корректировать» параметры классификатора, пока вы не достигните желаемой точности (т. к. маловероятно, что классификатор будет соответствовать всем вашим требованиям с первого же запуска).
Ниже будет представлен пример работы машинного обучения от обработки данных и до оценки.
Древа принятия решений
Древо решений представляют в форме 2-ичного древа, знакомого по структурам данных и алгоритмам. Здесь любой узел — это входная переменная и точка разделения для этой переменной, но при условии, что переменная является числом.
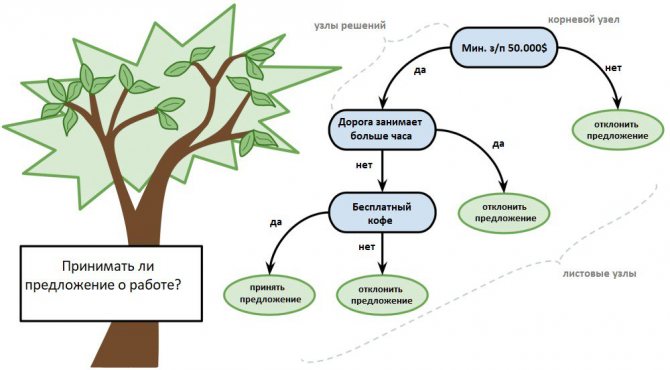

В качестве выходных переменных выступают листовые узлы, используемые для предсказания. Последние выполняются посредством прохода по древу к листовому узлу с последующим выводом значений класса на данном узле.
Древа быстро обучаются, точны для большого спектра круга задач, плюс не нуждаются в особой подготовке данных.
Реализация образца классификации
# Импорт всех нужных библиотек import pandas as pd from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC
Поскольку набор данных iris достаточно распространён, в Scikit-Learn он уже присутствует, достаточно лишь заложить эту команду:
sklearn.datasets.load_iris
Тем не менее, тут ещё нужно подгрузить CSV-файл, который можно скачать здесь.
Этот файл нужно поместить в ту же папку, что и Python-файл. В библиотеке Pandas есть функция read_csv(), которая отлично работает с загрузкой данных.
data = pd.read_csv(‘iris.csv’) # Проверяем, всё ли правильно загрузилось print(data.head(5))
Благодаря тому, что данные уже были подготовлены, долгой предварительной обработки они не требуют. Единственное, что может понадобиться — убрать ненужные столбцы (например ID) таким образом:
data.drop(‘Id’, axis=1, inplace=True)
Теперь нужно определить признаки и метки. С библиотекой Pandas можно легко «нарезать» таблицу и выбрать определённые строки/столбцы с помощью функции iloc():
# «.iloc» принимает row_indexer, column_indexer X = data.iloc[:,:-1].values # Теперь выделим нужный столбец y = data[‘Species’]
Код выше выбирает каждую строку и столбец, обрезав при этом последний столбец.
Выбрать признаки интересующего вас набора данных можно также передав в скобках заголовки столбцов:
# Альтернативный способ выбора нужных столбцов: X = data.iloc[‘SepalLengthCm’, ‘SepalWidthCm’, ‘PetalLengthCm’]
После того, как вы выбрали нужные признаки и метки, их можно разделить на тренировочные и тестовые наборы, используя функцию train_test_split():
# test_size показывает, какой объем данных нужно выделить для тестового набора # Random_state — просто сид для случайной генерации # Этот параметр можно использовать для воссоздания определённого результата: X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=27)
Чтобы убедиться в правильности обработки данных, используйте:
print(X_train) print(y_train)
Теперь можно создавать экземпляр классификатора, например метод опорных векторов и метод k-ближайших соседей:
SVC_model = svm.SVC() # В KNN-модели нужно указать параметр n_neighbors # Это число точек, на которое будет смотреть # классификатор, чтобы определить, к какому классу принадлежит новая точка KNN_model = KNeighborsClassifier(n_neighbors=5)
Теперь нужно обучить эти два классификатора:
SVC_model.fit(X_train, y_train) KNN_model.fit(X_train, y_train)
Эти команды обучили модели и теперь классификаторы могут делать прогнозы и сохранять результат в какую-либо переменную.
SVC_prediction = SVC_model.predict(X_test) KNN_prediction = KNN_model.predict(X_test)
Теперь пришло время оценить точности классификатора. Существует несколько способов это сделать.
Нужно передать показания прогноза относительно фактически верных меток, значения которых были сохранены ранее.
# Оценка точности — простейший вариант оценки работы классификатора print(accuracy_score(SVC_prediction, y_test)) print(accuracy_score(KNN_prediction, y_test)) # Но матрица неточности и отчёт о классификации дадут больше информации о производительности print(confusion_matrix(SVC_prediction, y_test)) print(classification_report(KNN_prediction, y_test))
Вот, к примеру, результат полученных метрик:
SVC accuracy: 0.9333333333333333 KNN accuracy: 0.9666666666666667
Поначалу кажется, что KNN работает точнее. Вот матрица неточностей для SVC:
[[ 7 0 0] [ 0 10 1] [ 0 1 11]]
Количество правильных прогнозов идёт с верхнего левого угла в нижний правый. Вот для сравнения метрики классификации для KNN:
precision recall f1-score support Iris-setosa 1.00 1.00 1.00 7 Iris-versicolor 0.91 0.91 0.91 11 Iris-virginica 0.92 0.92 0.92 12 micro avg 0.93 0.93 0.93 30 macro avg 0.94 0.94 0.94 30 weighted avg 0.93 0.93 0.93 30
Примечания к алгоритму
Линейная регрессия
Как мы уже говорили, линейная регрессия рассматривает данные линейно (или в плоскости, или в гиперплоскости). Это удобная и быстрая «рабочая лошадка», но для некоторых проблем она может быть чересчур простой. Здесь вы найдете руководство по линейной регрессии.
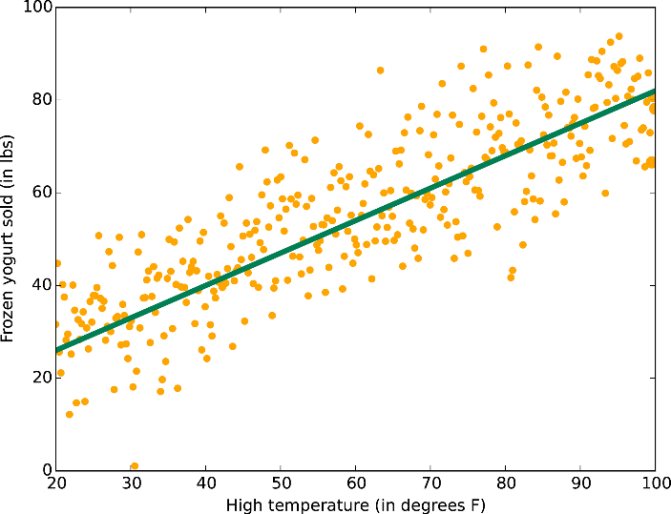

Данные с линейным трендом
Логистическая регрессия
Пусть слово «регрессия» в названии не вводит вас в заблуждение. Логистическая регрессия — это очень мощный инструмент для двухклассовой и многоклассовой классификации. Это быстро и просто. Поскольку вместо прямой линии здесь используется кривая в форме буквы S, этот алгоритм прекрасно подходит для разделения данных на группы. Логистическая регрессия ограничивает линейный класс, поэтому вам придется смириться с линейной аппроксимацией.
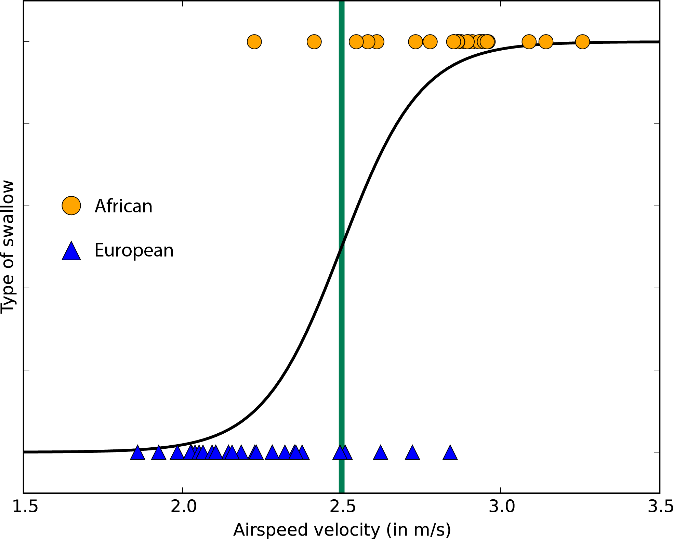

Логистическая регрессия для двухклассовых данных всего с одним признаком — граница класса находится в точке, где логистическая кривая близка к обоим классам
Деревья, леса и джунгли
Леса решающих деревьев (регрессия, двухклассовые и многоклассовые), джунгли решающих деревьев (двухклассовые и многоклассовые) и улучшенные деревья принятия решений (регрессия и двухклассовые) основаны на деревьях принятия решений, базовой концепции машинного обучения. Существует много вариантов деревьев принятия решений, но все они выполняют одну функцию — подразделяют пространство признаков на области с одной и той же меткой. Это могут быть области одной категории или постоянного значения, в зависимости от того, используете ли вы классификацию или регрессию.

Дерево принятия решений подразделяет пространство признаков на области с примерно одинаковыми значениями
Поскольку пространство признаков можно разделить на небольшие области, это можно сделать так, чтобы в одной области был один объект — это грубый пример ложной связи. Чтобы избежать этого, крупные наборы деревьев создаются таким образом, чтобы деревья не были связаны друг с другом. Таким образом, «дерево принятия решений» не должно выдавать ложных связей. Деревья принятия решений могут потреблять большие объемы памяти. Джунгли решающих деревьев потребляют меньше памяти, но при этом обучение займет немного больше времени.
Улучшенные деревья принятия решений ограничивают количество разделений и распределение точек данных в каждой области, чтобы избежать ложных связей. Алгоритм создает последовательность деревьев, каждое из которых исправляет допущенные ранее ошибки. В результате мы получаем высокую степень точности без больших затрат памяти. Полное техническое описание смотрите в научной работе Фридмана.
Быстрые квантильные регрессионные леса — это вариант деревьев принятия решений для тех случаев, когда вы хотите знать не только типичное (среднее) значение данных в области, но и их распределение в форме квантилей.
Нейронные сети и восприятие
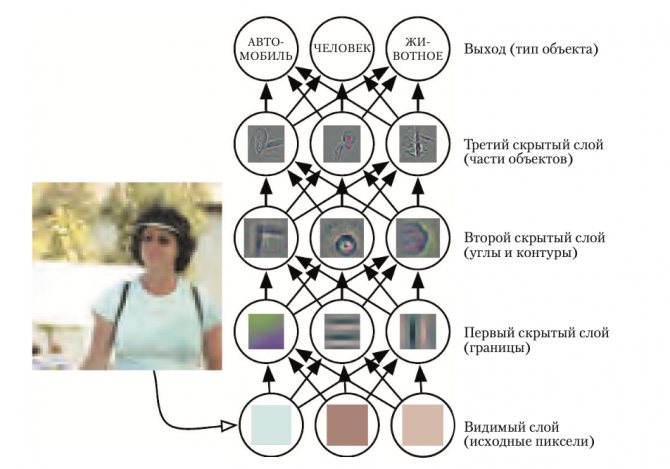
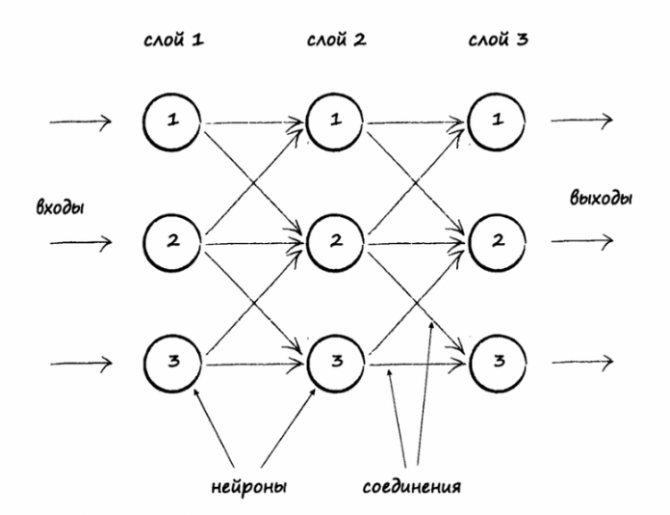
Нейронные сети — это алгоритмы обучения, которые созданы на основе модели человеческого мозга и направлены на решение многоклассовой, двухклассовой и регрессионной задач. Их существует огромное множество, но в машинном обучении Azure нейронные сети принимают форму направленного ациклического графика. Это означает, что входные признаки передаются вперед через последовательность уровней и превращаются в выходные данные. На каждом уровне входные данные измеряются в различных комбинациях, суммируются и передаются на следующий уровень. Эта комбинация простых расчетов позволяет изучать сложные границы классов и тенденции данных будто по волшебству. Подобные многоуровневые сети выполняют «глубокое обучение», которое служит источником вдохновения для технических отчетов и научной фантастики.
Но такая производительность обходится не бесплатно. Обучение нейронных сетей занимает много времени, особенно для крупных наборов данных с множеством признаков. В них больше параметров, чем в большинстве алгоритмов, и поэтому подбор параметров значительно увеличивает время обучения. А для перфекционистов, которые хотят указать собственную структуру сети, возможности практически не ограничены.
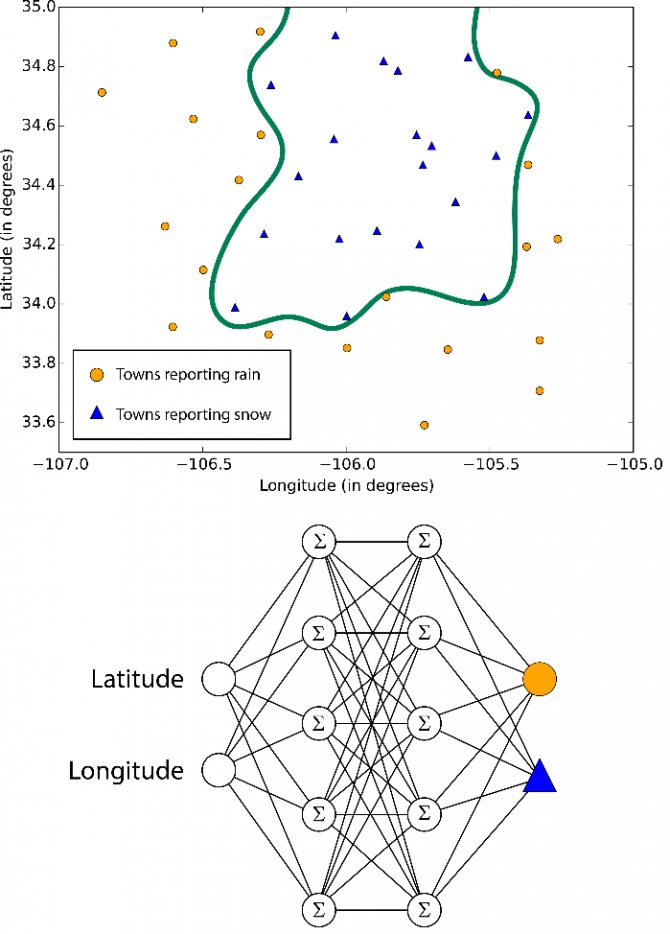

Границы, изучаемые нейронными сетями, бывают сложными и хаотичными
Однослойный перцептрон — это ответ нейронных сетей на увеличение времени обучения. В нем используется сетевая структура, которая создает линейные классовые границы. По современным стандартам звучит примитивно, но этот алгоритм давно проверен на деле и быстро обучается.
Методы опорных векторов
Методы опорных векторов находят границу, которая разделяет классы настолько широко, насколько это возможно. Когда невозможно четко разделить два класса, алгоритмы находят наилучшую границу. Двухклассовый метод опорных векторов делает это с помощью прямой линии (говоря на языке методов опорных векторов, использует линейное ядро). Благодаря линейной аппроксимации обучение выполняется достаточно быстро. Особенно интересна функция работы с объектами с множеством признаков, например, текстом или геномом. В таких случаях опорные векторные машины могут быстрее разделить классы и отличаются минимальной вероятностью создания ложной связи, а также не требуют больших объемов памяти.
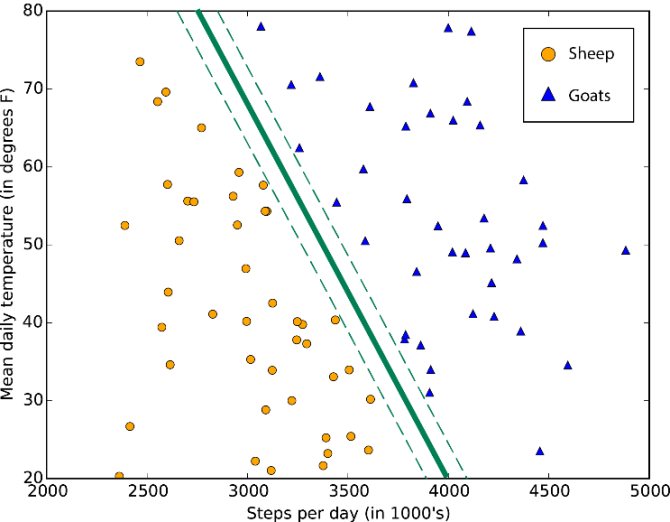

Стандартная граница класса опорной векторной машины увеличивает поле между двумя классами
Еще один продукт от Microsoft Research — двухклассовые локальные глубинные методы опорных векторов. Это нелинейный вариант методов опорных векторов, который отличается скоростью и эффективностью памяти, присущей линейной версии. Он идеально подходит для случаев, когда линейный подход не дает достаточно точных ответов. Чтобы обеспечить высокую скорость, разработчики разбивают проблему на несколько небольших задач линейного метода опорных векторов. Подробнее об этом читайте в полном описании.
С помощью расширения нелинейных методов опорных векторов одноклассовая машина опорных векторов создает границу для всего набора данных. Это особенно полезно для фильтрации выбросов. Все новые объекты, которые не входят в пределы границы, считаются необычными и поэтому внимательно изучаются.
Байесовские методы
Байесовские методы отличаются очень нужным качеством: они избегают ложных связей. Для этого они заранее делают предположения о возможном распределении ответа. Также для них не нужно настраивать много параметров. Машинное обучение Azure предлагает Байесовские методы как для классификации (двухклассовая классификация Байеса), так и для регрессии (Байесова линейная регрессия). При этом предполагается, что данные можно разделить или расположить вдоль прямой линии.
Кстати, точечные машины Байеса были разработаны в Microsoft Research. В их фундаменте лежит великолепная теоретическая работа. Если вас заинтересует эта тема, читайте статью в MLR и блог Криса Бишопа (Chris Bishop).
Оценка классификатора
Когда дело доходит до оценки точности классификатора, есть несколько вариантов.
Точность классификации
Точность классификации измерять проще всего, и поэтому этот параметр чаще всего используется. Значение точности — это число правильных прогнозов, делённое на число всех прогнозов или, проще говоря, отношение правильных прогнозов ко всем.
Хоть этот показатель и может быстро дать вам явное представление о производительности классификатора, его лучше использовать, когда каждый класс имеет хотя бы примерно одинаковое количество примеров. Так как такое будет случаться редко, рекомендуется использовать другие показатели классификации.
Логарифмические потери
Значение Логарифмических Потерь (англ. Logarithmic Loss) — или просто логлосс — показывает, насколько классификатор «уверен» в своём прогнозе. Логлосс возвращает вероятность принадлежности объекта к тому или иному классу, суммируя их, чтобы дать общее представление об «уверенности» классификатора.
Этот показатель лежит в промежутке от 0 до 1 — «совсем не уверен» и «полностью уверен» соответственно. Логлосс сильно падает, когда классификатор сильно «уверен» в неправильном ответе.
Площадь ROC-кривой (AUC)
Такой показатель используется только при бинарной классификации. Площадь под ROC-кривой представляет способность классификатора различать подходящие и не подходящие какому-либо классу объекты.
Значение 1.0: вся область, попадающая под кривую, представляет собой идеальный классификатор. Следовательно, 0.5 означает, что точность классификатора соответствует случайности. Кривая рассчитывается с учётом точности и специфичности модели. Подробнее о расчётах можно прочитать здесь.
Матрица неточностей
Матрица неточностей (англ. Confusion Matrix) — это таблица или диаграмма, показывающая точность прогнозирования классификатора в отношении двух и более классов. Прогнозы классификатора находятся на оси X, а результат (точность) — на оси Y.
Ячейки таблицы заполняются количеством прогнозов классификатора. Правильные прогнозы идут по диагонали от верхнего левого угла в нижний правый. Про это можно почитать в данной статье.
Отчёт о классификации
В библиотеке Scikit-Learn уже встроена возможность создавать отчёты о производительности классификатора. Эти отчёты дают интуитивно понятное представление о работе модели.