Дюрация облигации – это срок, по истечении которого инвестор сможет полностью окупить свои первоначальные вложения. Рассчитывается по достаточно сложной формуле, запоминать которую не обязательно. Важно лишь понимать, что дюрация исчисляется в годах либо в днях и определяется путем вычисления средневзвешенной величины.
Главный показатель, который характеризует дюрация, – это процентный риск. Инвестору, в портфеле которого есть долговые обязательства, необходимо иметь общее представление о том, как вычисляется дюрация облигации. Для расчета можно использовать различные онлайн-сервисы.
В этой статье мы разберем, что такое дюрация облигации простыми словами, приведем формулы и рассчитаем этот показатель на примерах.
Для чего нужна и где применяется

Итак, дюрация облигации – это срок окупаемости вложений в ценную бумагу. Для облигации с нулевым купоном эта величина равна сроку жизни долгового обязательства. Мы будем рассматривать подробно дюрацию купонной облигации и для начала приведем основные определения, которые нам понадобятся.
Облигация – это долговое обязательство государства или компании, по которому эмитент (заемщик) обязуется вернуть приобретателю (кредитору) номинальную стоимость ценной бумаги плюс процент (купон) в течение определенного срока.
Купон – это вознаграждение по облигации, выраженное в процентах к ее номиналу.
Накопленный купонный доход (НКД) – это сумма всех выплат по купону. Такие выплаты могут производиться с различной периодичностью:
- ежегодно;
- раз в полгода;
- ежеквартально.
Чем чаще производятся выплаты, тем сложнее расчет дюрации.
Ставка дисконтирования – это процент ожидаемой прибыли на будущее.
Кроме облигаций, дюрация применяется также для расчета срока окупаемости портфелей, кредитов и других долговых обязательств, инвестиционных проектов. С помощью этого показателя можно рассчитать срок погашения задолженности кредитором.
Где посмотреть
Указанные выше формулы я привела только с целью математической иллюстрации показателя. Некоторые люди лучше понимают суть процесса, когда им раскладывают его в цифрах. В практике инвестирования инвестор пользуется уже готовыми значениями, которые можно найти в нескольких источниках.
- Калькулятор МосБиржи – очень удобный инструмент, который дает абсолютно всю необходимую информацию
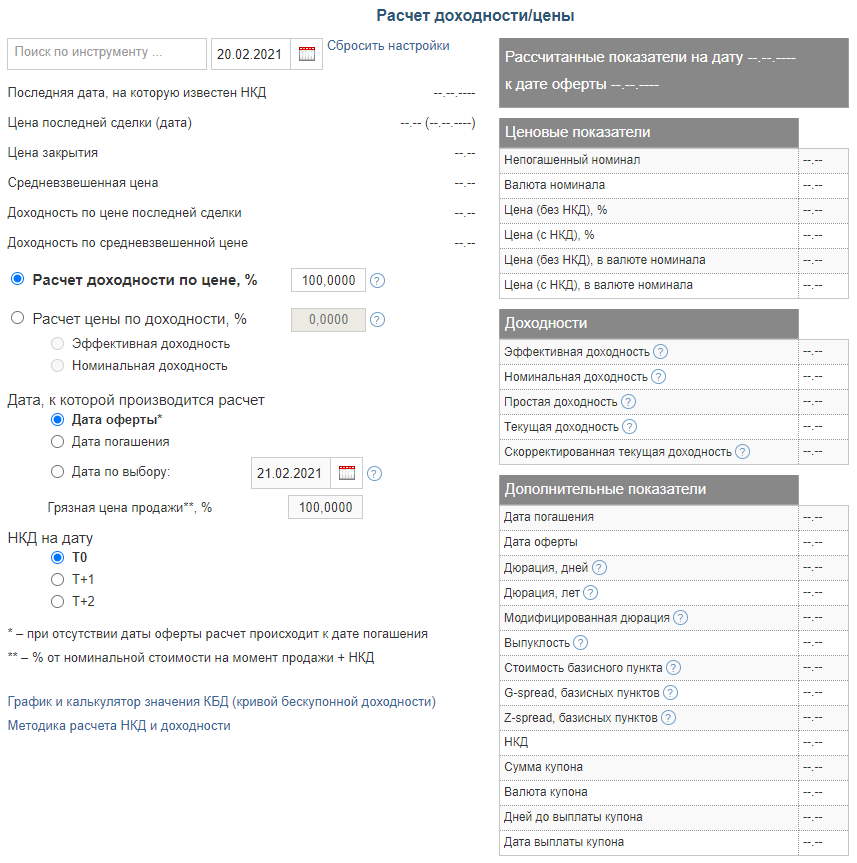

- Калькулятор на сайте rusbonds.ru – считает все параметры ценной бумаги

- Облигационный калькулятор Cbonds – есть подробная инструкция, где найти и как им пользоваться

- Инвестиционный портал smart-lab – показывает только дюрацию Маколея в днях

Эффективная дюрация и оферта
Более точной является формула эффективной дюрации облигаций, где учитываются изменения процентной ставки как в большую, так и в меньшую сторону. Эта формула подходит для облигаций с офертой, по которым предусмотрена возможность выкупа до срока погашения.
\[ D_e=\frac{P_{i-} – P_{i+}}{P_0*(i_+ – i_-)} , где \]
\( P_{i-} \) - рыночная цена в случае понижения ставок;
\( P_{i+} \)- рыночная цена в случае повышения ставок;
\( P_0 \)– исходная цена;
\( i_+ \)- размер повышенной ставки;
\( i_- \)- размер пониженной ставки.
Предположим, что ставка может измениться на 2 % в большую и на 3 % в меньшую сторону. Тогда, используя предыдущие расчеты, получим:
\( P_{i+} \)=25-(25*1,39*2/100)=1 826 руб. (24,34 $ или 706 грн.);
\( P_{i-} \)=25+(25*1,39*3/100)=1 953 руб. (26,04 $ или 755 грн.);
\( i_+ \)= 12 %;
\( i_- \)= 7 %.
\[ D_e=\frac{26,04-24,34}{25*(12-7)}=0,01 \]
Значение, близкое к нулю, говорит о низкой чувствительности рыночной стоимости долгового обязательства к изменению процентных ставок. Простыми словами, низкая дюрация – это показатель низкого уровня риска.
Соответственно, облигация с большей дюрацией представляет более высокий риск и более длительный срок окупаемости.
Этой формулой следует пользоваться, если правительство готовит постановления об изменении ставки Центробанка.
Модифицированная дюрация
Чтобы понять, на сколько процентов изменится рыночная цена облигации при повышении процентных ставок, используется модифицированная дюрация. Она отражает процентный риск облигации.


Источник: https://fs.moex.com/files/6908/
В нашем примере с ОФЗ 26211 дюрация Маколея D = 544 дня, если перевести значение в года, то 1,49. Y = 7,12% и n = 2, т.к. купоны выплачивают раз в полгода. Подставляем все значения в формулу:
И получаем 1,43. Это число означает, что при изменении требуемой доходности на 1%, рыночная цена облигации изменится на 1,43%.
Предположим, что на заседании ЦБ было принято решение повысить ключевую ставку на 5 б.п. Как это отразится на цене нашей облигации?
Для этого нужно использовать формулу стоимости базисного пункта:


Источник: https://fs.moex.com/files/6908/
В нашем примере с ОФЗ 26211, MD = 1,43, P = 100,9%, A = 2,89%. Подставляем все в формулу:
И получим стоимость изменения базисного пункта 1,48% или 0,0148. Т.е. При увеличении нормы доходности на 5 б.п. итоговая рыночная стоимость облигации снизится на 5*1,48 = 7,4%.
Как и в случае с дюрацией, модифицированную дюрацию и стоимость базисного пункта считать вручную не нужно, т.к. их можно найти в калькуляторе Московской биржи.
Дюрация портфеля облигаций


Дюрация портфеля рассчитывается путем определения средневзвешенной величины сроков окупаемости ценных бумаг, входящих в портфель. При этом учитывается их процентное соотношение.
Пример. Портфель инвестора состоит из пяти видов ОФЗ.
| Облигация | D, лет | Доля в портфеле, % |
| 1 | 2,68 | 20 |
| 2 | 1,92 | 20 |
| 3 | 1,89 | 20 |
| 4 | 2,14 | 20 |
| 5 | 2,87 | 20 |
\[ Dport=2,68*0,2+1,92*0,2+1,89*0,2+2,14*0,2+2,87*0,2=2,3 г. \]
Таким образом, дюрация портфеля – это средний срок, в течение которого инвестор возместит первоначальные вложения.
Здесь нужно учитывать то, что если ребалансировка производилась до срока погашения, то дюрация портфеля облигаций должна рассчитываться заново. При этом показатель по проданным ценным бумагам должен приниматься как фактический срок нахождения в портфеле. Простыми словами, если облигация со сроком погашения 3 года была продана через 2, то ее дюрация составит 2 года. Размер денежного потока следует исчислять с учетом НКД.
Бессрочные облигации
Бессрочная облигация подходит вкладчикам, которые хотят довольно долго получать стабильную прибыль. Бумага не предусматривает выкуп номинала. Ее владельцу полагается только купонная прибыль. Но в условиях эмиссии может быть сказано, что ДО имеет определенный срок. Например, принудительное погашение (колл-опцион) ОФЗ (КО) производится спустя 10 лет.
Первое размещение вечных облигаций на Мосбирже провел ВТБ банк в 2012 году. Позже на рынок вышел Газпромбанк и Промсвязьбанк. В 2016 году финансовые инструменты начал использовать Альфа-банк и ТКС банк (Тинькофф).
Вечные облигации выпускались в виде евробондов в иностранной валюте. Цена минимального лота начиналась от 100 000 долларов. Купоны вечных облигаций могли быть фиксированными или плавающими. ВТБ банк и Газпромбанк привязывали купонные выплаты к 5 и 10-летним гособлигациям США (+ 7,1 и 8,1% соответственно). Колл-опционы были запланированы на 2022 и 2022 гг.
Рублевые облигации сумел выпустить только Россельхозбанк. С 2018 года на рынок могут выходить не только банки, но и другие финансовые компании.
В 2022 году ОАО «РЖД» разместило евробонды серии 001Б-04 объемом 80 млрд. руб. Ставка купона – 7,25% годовых. По ценным бумагам предусмотрены колл-опционы каждые пять лет. В качестве организаторов выступило несколько организаций – ВТБ Капитал, МКБ, Sberbank CIB, Промсвязьбанк, БК «Регион» и Россельхозбанк.
Бессрочная облигация считается довольно выгодным инструментом вложения денег. Однако бумага не застрахована от всех рисков. При банкротстве компании (эмитента) она не предоставляет заметных выгод своему владельцу.
Дюрация проекта
Срок окупаемости определяется не только для инвестиций в ценные бумаги, но и для различных бизнес-проектов.
Пример. Компания запускает новый бизнес проект с начальным размером инвестиций – 22 500 000 руб. (300 000 $ или 8 700 000 грн.). Ставка дисконтирования – 11 %.
Доходы от проекта составили:
| Год | Размер дохода, $ |
| 1 | 25000 |
| 2 | 46000 |
| 3 | 60000 |
| 4 | 85000 |
| 5 | 120000 |
Рассчитаем суммы денежных потоков для каждого года:
PV1=25000/(1+0,110)=1 689 225 руб. (22 523 $ или 653 167 грн.);
PV2=46000/(1+0,110)=3 108 075 руб. (41 441 $ или 1 201 789 грн.);
PV3=60000/(1+0,110)=4 054 050 руб. (54 054 $ или 1 567 566 грн.);
PV4=85000/(1+0,110)=5 743 275 руб. (76 577 $ или 2 220 733 грн.);
PV5=120000/(1+0,110)=8 108 100 руб. (108 108 $ или 3 135 132 грн.).
\[ D=\frac{1*22523+2*41441+3*54054+4*76577+5*108108}{22523+41441+54054+76577+108108}=3,68 г. \]
Таким образом, проект окупится на четвертом году.
Чтобы рассчитать дюрацию кредита, можно взять любой график аннуитетных платежей и складывать их суммы до тех пор, пока значение не будет равно телу кредита. Срок платежа, в котором сумма выплаченных заемщиком средств достигнет размера основного долга, и будет искомым значением. При этом банк при определении этого срока учитывает инфляцию и ожидаемую прибыль.
Пример расчета дюрации
Смоделируем схемы расчета ДО по двум видам похожих инструментов. Для этого сравним ОФЗ номиналом по 1 тыс. руб. Срок выкупа – 12 месяцев. Прибыльность – 10%. Сумма выплат за год – 100 р. Отличается только периодичность денежных поступлений:
- Купоны выдаются 2 раза в год. Стоимость купона – 50 р.
- Выплаты делаются ежеквартально (4 раза за год). Цена купона – 25 р.
В таблице указаны основные параметры инструментов:
| Показатель | №1 | №2 |
| Номинал, руб. | 1 000 | 1 000 |
| Размер купона, в руб. | 50 | 25 |
| Количество выплат | 2 | 4 |
| График платежей | — | — |
| 01.04.2020 | — | 25 |
| 01.07.2020 | 50 | 25 |
| 01.10.2020 | 25 | |
| 01.01.2021 | 50 | 25 |
| Сумма выкупа, руб. | 1 100 | 1 100 |
Формула расчета №1:
Общее количество дней дюрации составляет менее 1 года. Расчеты делались на основании годовых показателей, но без учета дисконтирования. Это упростило задачу и не отразилось на конечном результате.
Формула расчета №2:
Значение во втором примере немного меньше. Причина – более быстрый возврат купонных выплат. Стоимость финансового инструмента окупится быстрее.
Инвестору выгоднее выбирать ОФЗ с меньшей ДО. Это позволит снизить риски и обеспечит активное движение капитала. Следовательно, инвестор получит большую прибыль за счет повторного вложения средств.
Повышенный риск присущ и бескупонным облигациям. По ним нет промежуточных платежей. Выплата дохода делается единовременно.
По эмиссии облигаций с определенным до даты выкупа денежным потоком дюрация рассчитывается к погашению. По выпуску бумаг с неисполненными офертами и частично определенным денежным потоком показатель рассчитывается к оферте.
Свойства дюрации
Обобщим основные свойства дюрации облигаций:
- Для облигаций с купоном дюрация всегда меньше их срока жизни. Простыми словами, ценная бумага должна окупить себя до установленного срока погашения.
- Для бескупонных облигаций дюрация равна сроку погашения.
- Цена обязательства увеличивается с уменьшением купонных выплат. И наоборот, если купонные выплаты повышаются, падает рыночная стоимость ценной бумаги.
- Облигация с большей дюрацией имеет более высокий уровень процентного риска.
Взаимосвязь выпуклости и дюрации
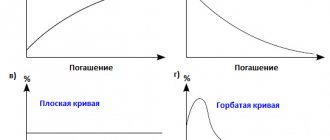
Если инвестор графически представит получение доходности от облигаций, то получит не прямую линию, а выпуклую кривую, изгиб или «выпуклость» которой зависит от доходности ценной бумаги.
Понятие «выпуклость» — это финансовый термин и характеризуют зависимость стоимости облигации от ее доходности. «Выпуклость» напрямую связана с дюрацией и отражает свойство ее изменения – чем больше скорость изменения, тем сильнее изменяется дюрация.
График выпуклости выглядит следующим образом:
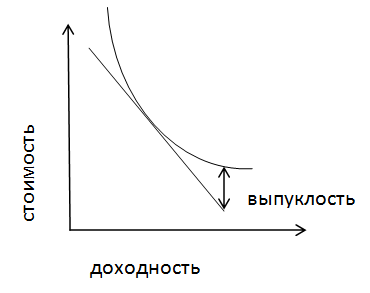

Для инвестора значение «выпуклости» говорит о том, что чем больше выпуклость конкретной облигации, тем быстрее растет доходность, но и тем ниже становится стоимость облигации.
Что такое «выпуклость» облигации


Мы уже знаем, что дюрация облигации определяет риск изменения рыночной стоимости в зависимости от размера денежных потоков.
Если имеются две ценные бумаги с одинаковым рассчитанным сроком окупаемости, тогда инвестор обращает внимание на показатель второго порядка – выпуклость облигации, т.е. чувствительность рыночной цены к изменению размера процентных ставок.
Если изменение ставок оказывает существенное влияние на волатильность облигаций, то такая бумага отличается негативной выпуклостью. И наоборот, менее чувствительные к изменению ставок обязательства имеют позитивную выпуклость и низкий уровень риска.
Дюрация Маколея: формула расчёта
Наиболее известный способ расчета дюрации — формула Маколея. Дюрация Маколея – это средневзвешенное время до получения купонов и номинала. Дюрация Маколея измеряется в годах.
В формуле Маколея каждый платеж по облигации получает свой вес в зависимости от срока, когда он будет получен по методу дисконтирования: чем раньше поступает платеж, тем выше его вес. Сумма взвешенных платежей делится на текущую рыночную цену и получается искомый результат.


Формула является довольно сложной и запутанной, поэтому обычные инвесторы к самостоятельным расчетам по ней прибегают крайне редко, предпочитая использовать специальные сервисы с готовыми значениями по каждому виду облигаций. Как раз это значение можно увидеть в терминале в QUIK.
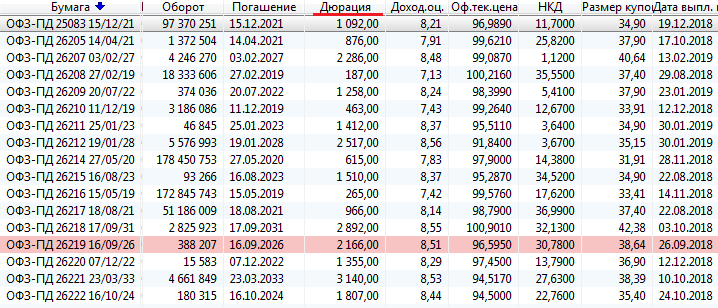

Упрощенное объяснение формулы:
В числителе: Сумма из (поступление по облигации * время поступления) Знаменатель: Цена облигации + НКД
Поступления по облигациям – это все будущие платежи: купоны и погашение. Так как это будущие платежи разного времени, нужно каким-то образом привести их к сегодняшнему дню. С точки зрения математики, эти платежи надо освободить от доходности, то есть дисконтировать. Это делается потому, что 1000 рублей сейчас НЕ РАВНЫ этой сумме через 1 год, через 2 и т.п. Дисконтирование — это процесс, обратный начислению процентов.
Более важно просто понимать, что дюрация облигаций зависит от цены и оставшегося до погашения срока, при этом:
- При неизменной цене, если срок до погашения уменьшается, дюрация тоже уменьшается.
- При неизменном сроке, если цена на облигацию вырастает, то дюрация тоже уменьшается; если же цена снижается, то увеличивается.
Таким образом, дюрация облигаций постоянно меняется, она пересчитывается каждый день и каждый день будет разной.
Как изменение процентной ставки влияет на цену облигаций
Динамика рыночных цен на облигации во многом зависит от изменения процентных ставок. При этом существует обратная зависимость: при росте ставок рыночная цена снижается, при падении ставок – растет.
Эта зависимость далеко не всегда равнозначна. К примеру, если ставки упали на 5 %, то стоимость ценной бумаги может вырасти на те же 5 %. Если же ставки выросли на 5 % – облигация подешевеет на 4 %.
Решающее влияние на доходность долговых обязательств оказывает ключевая ставка Центробанка. Если размер ключевой ставки вырос, купонные облигации падают в цене. При падении ключевой ставки рыночная стоимость таких ценных бумаг растет.
Формула денежной дюрации (по Маколею) не учитывает изменение ставок. Для расчета срока окупаемости инвестиций при переменных ставках лучше использовать показатели эффективной дюрации и модифицированной дюрации облигаций.
Дюрация. Что это такое и почему она важна
Когда разговор заходит о долговых инструментах часто можно встретить такой термин, как дюрация. В обзоре мы разберем, что обозначает этот показатель и как его применять на практике.
При покупке облигации инвестор берет на себя два ключевых риска: кредитный — риск дефолта эмитента, и процентный — риск колебаний рыночной стоимости бумаги в ответ на изменение уровня процентных ставок в экономике.
Пример процентного риска: Есть облигация с фиксированным купоном, торгуемая по номиналу 100% с доходностью 8% в год. Из-за изменения ситуации на рынке, доходность по аналогичным инструментам выросла до 10%. Соответственно, чтобы наша бумага была интересна инвесторам, она должна обеспечивать аналогичную доходность. Но так как купон уже был ранее зафиксирован на уровне 8%, то такая доходность может быть обеспечена только за счет снижения стоимости покупки облигации. Рыночная цена бумаги снижается и становится меньше номинала. В этом и заключается процентный риск облигаций — их цена падает при росте доходностей на рынке и, наоборот, растет в случае их снижения.
Для измерения и сравнения между собой процентных рисков разных долговых бумаг и был веден показатель дюрации.
Как измерить уровень процентного риска
Первым ключевым фактором, который влияет на процентный риск, является срок до погашения.
Пример: есть две абсолютно одинаковые облигации с погашением через 3 года и 5 лет. Из-за роста ключевой ставки на 1% доходности по таким облигациям на рынке также выросли на 1%. Соответственно, компенсировать разницу в доходности к погашению, 3-летняя облигация должна торговаться на 1%*3 года = 3% ниже своей начальной стоимости, 5-летняя бумага — на 1%*5 лет = 5%.
Пример является упрощенным, но наглядно показывает, как соотносится процентный риск со сроком до погашения. Однако помимо срока до погашения имеет значение и размер купона. При прочих равных более привлекательными для инвесторов будут бумаги с большим размером купона. Это значит, что облигация с купоном 20% в случае роста ставок меньше просядет в цене, чем облигация с купоном 10% при одинаковом сроке до погашения.
В 1938 г. Фредерик Маколей разработал свой метод, как учитывать купоны при оценке процентного риска. Он предложил сравнивать облигации не по сроку до погашения, а по средневзвешенному сроку до получения купонов и номинала.
В формуле Маколея каждый платеж по облигации получает свой вес в зависимости от срока, когда он будет получен по методу дисконтирования: чем раньше поступает платеж, тем выше его вес. Сумма взвешенных платежей делится на текущую рыночную цену и получается искомый результат. Новый показатель Маколей предложил называть дюрацией (от англ. duration — длительность).
где: P — текущая цена облигации;
r — доходность к погашению/оферте;
t — срок поступления платежа (купона или номинала);
N — номинал облигации (в деньгах);
C — купонный платеж;
n — количество платежей.
Дюрация Маколея является базовой для расчетов других показателей, связанных с волатильностью цены облигаций. Так как она представляет из себя временной период, она может измеряться в днях. Именно в таком виде ее можно увидеть в терминале QUIK.
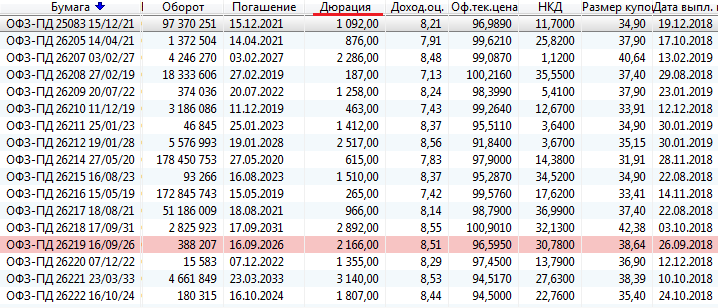

Чем выше дюрация облигационного выпуска, тем сильнее он реагирует на изменение требуемой доходности. Иными словами, чем выше дюрация, тем выше процентный риск.
Стоит отметить ряд особенностей, характерных для дюрации:
— При прочих равных, чем больше срок до погашения, тем выше дюрация.
— При прочих равных, чем выше величина купона и чем чаще он выплачивается, тем ниже дюрация.
— При прочих равных, чем выше доходность к погашению, тем ниже дюрация.
— Дюрация Маколея бескупонной облигации равна сроку до погашения.
Применение на практике
На практике обычно используется модифицированная дюрация (МД), которая рассчитывается на основе дюрации Маколея по простой формуле:
Учитывая, что в QUIK дюрация Маколея измеряется в днях, полученное значение необходимо разделить еще на 365. Для примера рассчитаем МД для выпуска ОФЗ-ПД 25083 по показателям из таблицы на предыдущей картинке. Получим 1092 / ((1+ 0,0821)*365) = 2,76.
Модифицированная дюрация является безразмерной величиной, а ее математический смысл заключается в следующем: модифицированная дюрация является приближенным изменением стоимости облигации в ответ на изменение доходности на 1% (100 базисных пунктов).
ΔP = -МД * Δy,
где ΔP — изменение стоимости облигации, Δy — изменение доходности.
По этой формуле можно оценить изменение стоимости облигации при небольших изменениях доходности.
Пример: Облигация с номиналом 1000 руб. торгуется по цене 101,7% (1017 руб.), с доходностью 8% и модифицированной дюрацией 1,72. Если доходности на рынке вырастут с 8% до 10%, то стоимость облигации изменится примерно на -1,72 * (0,1-0,08) = -0,0344 = -3,44%. Бумага будет торговаться по цене 1017 * (1- 0,0344) = 982,02 руб. (98,2% от номинала)
Модифицированная дюрация облигационного портфеля из нескольких бумаг упрощенно рассчитывается, как сумма произведений дюрации каждого выпуска на его долю:
Пример: составлен портфель из двух бумаг. Доля первой бумаги 30%, ее дюрация 0,8. Доля второй бумаги 70%, дюрация 1,4. Дюрация всего портфеля будет равна 0,3*0,8 + 0,7*1,4 = 1,22.
При формировании портфеля дюрация используется согласно следующей стратегии:
Если ожидается снижение уровня процентных ставок, то инвестору стоит повысить дюрацию портфеля, чтобы извлечь большую прибыль из-за роста цен.
Если ожидается рост процентных ставок, то стоит снизить дюрацию портфеля, чтобы сократить потери от снижения цен.
Если у вас нет сформированного мнения о будущей динамике процентных ставок, формируйте портфель так, чтобы его дюрация была примерно равна сроку предполагаемого инвестирования.
Важный момент: дюрация в терминале QUIK учитывает дюрацию по облигациям с переменным купоном до даты ближайшей оферты put. Но оферта call в терминале не учитывается. Дюрацию до оферты call можно рассчитать самостоятельно по формуле, либо посмотреть на специализированных ресурсах типа cbonds.ru и rusbonds.ru.
Выпуклость
Для обычного частного инвестора объем приведенный выше информации вполне достаточен, чтобы управлять процентным риском небольшого портфеля, используя дюрацию. Но для более точных расчетов, важность которых возрастает с ростом суммы и сроков инвестиций, необходимо познакомиться еще с одним понятием.
Как было указано ранее, модифицированная дюрация дает только приблизительную оценку и подходит лишь для небольших изменений доходности. Все дело в том, что зависимость цены облигации от ее доходности не линейная, а представляет из себя кривую:
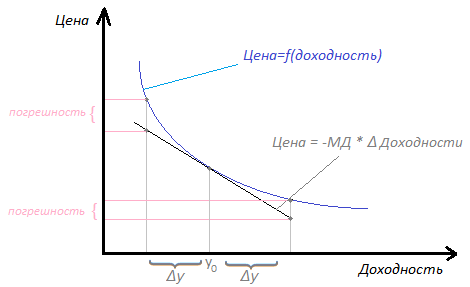

Таким образом, чем больше изменение процентной ставки, тем больше реальное изменение стоимости будет отклоняться от расчетного. Диапазон ставок, в котором погрешность можно считать несущественной, зависит от параметров конкретной облигации и объема средств, которые планируется в нее инвестировать.
Вторым важным моментом является несимметричность графика Цена/Доходность. При снижении процентной ставки на 1% цена вырастет больше, чем снизится при аналогичном росте ставки на 1%.
Для того чтобы снизить погрешность вычислений используют еще один параметр, характеризующий выпуклость кривой Цена/Доходность. Его так и называют выпуклость, или еще используется термин конвекция.
Математический смысл выпуклости выходит за рамки этой статьи, но для практического применения обычному частному инвестору он, в общем-то, ни к чему. Значение выпуклости можно найти на тех же специализированных ресурсах вроде rusbonds.ru или cbonds.ru. В расчеты выпуклость (Впкл) включается следующим образом:
Первое слагаемое этой формулы, которое вы уже видели ранее, называется процентное изменение цены, обусловленное дюрацией. Второе слагаемое, соответственно, процентное изменение цены, обусловленное выпуклостью.
Второе слагаемое корректирует рассчитанное по дюрации значение и вносит в него несимметричность. Положительная выпуклость, характерная для обыкновенных облигаций, корректирует результат в сторону роста цены и является позитивным моментом для инвестора.
Одновременное использование дюрации и выпуклости дает более корректное значение изменения доходности облигации в ответ на смещение процентных ставок.
При прочих равных большая выпуклость более выгодна для инвестора.
На графике хорошо видно, что при одинаковой дюрации более выпуклая облигация B оказывается выгоднее для инвестора при значительном изменении процентных ставок. При снижении ставок она быстрее растет в цене, а при их росте — медленнее теряет свою стоимость.
В случае если инвесторы на рынке ожидают высокой волатильности процентных ставок, участники рынка могут предпочитать среди бумаг с одинаковой дюрацией те, у которых более высокая выпуклость. Это будет отображаться в виде меньшей доходности таких облигаций.
И напротив, когда ожидается низкая волатильность ставок, инвесторам незачем жертвовать доходностью ради выпуклости и они переводят капитал в более доходные бумаги. Эту закономерность частный инвестор может использовать в качестве индикатора настроений на долговом рынке.
Выпуклость всего портфеля облигаций измеряется аналогично дюрации портфеля: выпуклость каждой бумаги умножается на её вес в портфеле и полученные значения складываются.
Особенности применения дюрации
Может возникнуть закономерный вопрос: почему бы вместо дюрации и выпуклости просто не использовать функцию Цена = f (доходность). Однако такие расчеты оказываются чересчур громоздкими даже при использовании вычислительной техники. Очень часто дюрация и выпуклость дают возможность получить хорошее приближение искомой величины с допустимым уровнем погрешности.
Приведенные показатели дюрации и выпуклости справедливы только для обыкновенных облигаций без встроенных опционов. Если изменение доходностей приводит к изменениям предполагаемых денежных потоков облигации, то меры дюрации и выпуклости применимы лишь в некоторых специфических случаях.
Понятие дюрации и оценка процентного риска долговых бумаг в целом не ограничивается приведенными в данном обзоре показателями. Однако для обычного частного инвестора этих понятий достаточно, чтобы разумно сформировать портфель облигаций с учетом процентного риска. В том случае если вы хотите еще глубже вникнуть в методики управления облигационным портфелем, рекомендуем ознакомиться со специализированной литературой, например, Фрэнк Фабоцци «Рынок облигаций. Анализ и стратегии».
Открыть счет
БКС Брокер
Пример определения дюрации
Рассмотрим пример, в котором рассчитаем дюрацию для «смешанного» портфеля, включающего купонные и бескупонные ОФЗ, а также корпоративные бумаги.
Итак, портфель инвестора выглядит следующим образом:
| Наименование ценной бумаги | Номинальная стоимость, $ | Рыночная цена, $ | Срок до погашения, лет | Купон, % | Количество выплат в год | Дюрация, лет | Доля в портфеле, % |
| ОФЗ | |||||||
| 1 | 12,5 | 12,6 | 6 | 7,75 | 2 | 0,07 | 5 |
| 2 | 12,5 | 13 | 7 | 11 | 3 | 0,07 | 5 |
| 3 | 12,5 | 11 | 2 | 2 | 10 | ||
| 4 | 12,5 | 14 | 9 | 10 | 1 | 0,16 | 10 |
| 5 | 12,5 | 17 | 10 | 9 | 3 | 0,04 | 10 |
| Корпоративные | |||||||
| ВЭБ | 12,5 | 12,5 | 5 | 11,6 | 1 | 0,30 | 10 |
| Газпром | 12,5 | 10,6 | 4 | 7,7 | 2 | 0,09 | 10 |
| Рольф | 12,5 | 11,5 | 2 | 9 | 4 | 0,09 | 10 |
| РЕСО-Лизинг | 12,5 | 12,3 | 2 | 9,7 | 2 | 0,18 | 10 |
| Гарант-Инвест | 12,5 | 11,2 | 2 | 13,5 | 4 | 0,12 | 10 |
| Тинькофф | 12,5 | 12,9 | 2 | 7,3 | 2 | 0,16 | 10 |
Мы видим, что все ценные бумаги, за исключением бескупонных, окупятся в первом году после приобретения. Следовательно, портфель состоит из низкорисковых облигаций.
По приведенной выше формуле рассчитаем дюрацию по портфелю и получим значение 0,14.
Зачем нужна дюрация и как ее использовать на практике при выборе облигаций
Теперь вы знаете, что такое дюрация и где ее можно найти. Так для чего же она нужна?
Как мы уже выяснили, дюрация показывает срок окупаемости вложений, на который влияют величина, периодичность купонных выплат, доходность и срок до погашения:
- чем больше размер купона, тем ниже дюрация, т.к. вы быстрее вернете свои вложенные средства;
- чем чаще выплаты, тем больше дюрация, т.к. выплаты будут более растянуты по времени;
- чем выше доходность до погашения, тем ниже дюрация;
- чем больше время до погашения, тем больше дюрация.
Исходя из вышесказанного можно сделать вывод, что тем ниже дюрация, тем лучше для инвестора, т.к. он быстрее вернет вложенные средства и поэтому риски будут ниже.
Как применять дюрацию на практике
Итак, обобщим понятие дюрации простыми словами, чтобы было понятно даже для детей: мы даем деньги в долг под процент и нам нужно знать, как скоро мы сможем вернуть свои средства так, чтобы не остаться в убытке. Понятно, что давая деньги в долг человеку под проценты или без них, мы всегда принимаем риск невозврата средств или просрочки.
В случае с ценными бумагами такой риск тоже имеется, но долговые бумаги имеют свой плюс: их можно продать до срока погашения по текущей рыночной цене.
Если вы приобретаете облигации и держите их до погашения, дюрация вам не особо и нужна. Но если вы являетесь трейдером, она вам необходима. Конечно, самостоятельно рассчитывать срок окупаемости бумаги по сложной формуле не нужно, т.к. это займет много времени и велика вероятность ошибки. Можно использовать специальные онлайн-сервисы и торговые терминалы.
Что такое дюрация простыми словами
Если говорить простым языком, то дюрация – это величина, которая связывает текущую стоимость облигации и купонный доход до ее погашения. Это некий период, за который кредитор сможет вернуть вложенные деньги. В большинстве случаев дюрация обозначается именно в днях.

Для чего нужна и где используется
Чтобы понять, для чего нужна дюрация, предлагаю погрузиться в следующую ситуацию.
Предположу, что у меня есть два возможных заемщика, каждый из них хочет взять кредит на год в размере 1000 руб. Но у меня только одна тысяча, поэтому мне придется выбирать.
- Первый предлагает мне 10 % годовых, но при этом проценты собирается выплачивать каждый месяц, т.е. платежами по 8,3 (3) руб.
- Второй предлагает вернуть мне деньги с большей доходностью, например 11 %, но собирается отдать всю сумму в конце периода через год.
У меня как инвестора возникает мысль, что если я буду получать по 8,3 (3) руб., то могу на них каждый раз покупать ОФЗ, по которым я буду получать 8 % годовых. Значит, после первого платежа я купил облигации на 8,3 (3) руб., мне на них пошли проценты, после второго платежа то же самое и т.д.
Вычисления непростые, поэтому поверьте на слово: на первом заемщике я смогу заработать около 10,366 %, а от второго получу 11 %. Выходит, что 2-й вариант для меня предпочтительнее, но разница не так велика, как казалось изначально.
Так вот дюрация нужна для того, чтобы не вычислять все это самому, а моментально видеть, как бумаги с совершенно разными условиями, сроками и рисками приводятся к общему знаменателю.
Где смотреть
В основном облигации торгуются через российских брокеров. Просматривать и анализировать величины дюрации удобнее всего через торговый терминал, предоставляемый финансовым агентом.
Если нет возможности подключиться к брокерским программам, то необходимые материалы можно также найти в интернете на специализированных сайтах. Доступ к некоторым платный, но есть и свободные ресурсы.
Процентные ставки
Получается, чем короче дюрация, тем меньшие риски несет инвестор. Но есть еще показатель изменения процентных ставок в будущем. Между ним и облигациями есть обратная зависимость: ставка поднимается, рыночная стоимость облигаций снижается. И наоборот. Например, есть 2 страны. В первой стране – все хорошо, значит, с каждым годом процентная ставка становится меньше. Сегодня она – 10 % годовых, а через год – всего 5. Это влияет на доходность и саму стоимость облигаций?
Текущие облигации дают доходность 10 % годовых. Через год, процентная ставка в стране упадет до 5 %. Значит и выпускающие ценные бумаги эмитенты будут предлагать за облигации те же 5 %. Больше – не разумно. Но ведь остаются бумаги, которые были выпущены ранее с доходностью в несколько раз выше! Логичнее покупать их? Но кто же отдаст такие хорошие облигации? Вот, чтобы уровнять среднюю доходность облигаций на рынке, рыночная стоимость уже выпущенных ранее ценных бумаг автоматически повысится. Примерный расчет таков: при снижении ставки на процент, стоимость облигаций вырастет на столько же за каждый год до погашения. Снижение процентной ставки на 2 % увеличивает стоимость облигаций на срок до погашения:
- 5-летних – на 10 %;
- 10-летних – на 20 %;
- 20-летних – на 40 %.
Поэтому, когда в стране действуют максимальные ставки, выгодно брать облигации с длительной дюрацией. При прогнозируемом падении ставок, ее изменение приведет к увеличению стоимости облигации. Чем больше дюрация, тем больший доход можно получить.
Но может быть и наоборот. При сильной инфляции в стране, ежегодно растет процентная ставка, а с ней – средняя доходность облигаций по рынку. Сегодня это 10 %, а через несколько лет можно ждать до 40 % и выше! Тогда наши ценные бумаги понемногу обесценятся. Например, куплены ценные бумаги номиналом в 1000 руб. с 20 % годовой доходностью. Через пару лет рынок наводнили новые облигации с 40 % годовой доходностью. Старые бумаги с купоном в 29 % никому не интересны. Чтобы нивелировать разрыв в доходности бумаг, приходится снижать их стоимость.
В итоге: бумаги с номиналом 1000 руб. два года назад, приносящие владельцу 20 % или 200 руб. прибыли ежегодно, сегодня, пусть и будут приносить те же 200 руб. в год, но оцениваться на рынке будут в 2 раза ниже. Поэтому при повышении процентных ставок в будущем, нужно обращать внимание на бумаги с минимальной дюрацией.
Подытожим
Сама по себе дюрация – это цифры, не более того. Ее польза в фильтрации ценных бумаг для покупки, если при равных условиях надо сделать выбор в пользу меньшего риска или высокой потенциальной прибыли. Например, есть желание вложиться на 10 лет в облигации федерального займа. На рынке их несколько десятков с разными купонами и рыночной стоимостью. На первый взгляд, стоит обратить внимание на текущую доходность: чем она выше, тем выгоднее для нас.
Но! Можно столкнуться с тем, что ценная бумага всегда погашается по номиналу в конце срока обращения. При этом, если текущая рыночная стоимость облигаций сильно превышает номинал (например, на 500 руб. при номинале в 1000), то при погашении бумаг, инвестору грозит убыток на эту разницу (- 500 руб.). И вся более высокая доходность будет съедена.
Для того, чтобы умело работать на фондовом рынке надо знать ряд правил:
- дюрация без купонной облигации всегда равна ее сроку до погашения;
- купонные долговые бумаги имеет дюрацию меньше срока своего обращения;
- чем меньше дюрация, тем ниже риски;
- облигации с высокой дюрацией сильнее реагируют на изменение процентных ставок в будущем, что приводит к изменению их рыночной стоимости;
- при прогнозировании снижения процентных ставок в будущем, максимально доходны бумаги с длительной дюрацией.
Обратите внимание вот на что. Если есть предпосылки для повышения процентных ставок – ваше предпочтение должно быть отдано бумагам с минимальной дюрацией. Именно они меньше всего реагируют на изменение рыночной цены. При этом дюрация может меняться ежедневно: сокращается срок возврата средств! Сократить дюрацию способен высокий уровень купонных платежей из-за более быстрого возврата вложений. Низкий – напротив, все увеличивает.